Республиканская олимпиада по математике, 2009 год, 9 класс

Задача №1. В треугольнике

$ABC$ вписанная окружность касается сторон

$BC$ ,

$CA$ и

$AB$ в точках

$A_1$ ,

$B_1$ и

$C_1$ соответственно. Обозначим ортоцентры треугольников

$AC_1B_1$ и

$CA_1B_1$ через

$H_1$ и

$H_2$ . Докажите, что четырехугольник

$AH_1H_2C$ — вписанный.
комментарий/решение(4)

Задача №2. В шахматном турнире участвуют 11 человек. За весь турнир каждый игрок играет с каждым другим ровно одну партию. В каждой партии игроку за выигрыш начисляется —

$1$ очко, за ничью —

$0,\!5$ очков, а за проигрыш — 0 очков. Если по окончании турнира игрок набирает не менее

$75\%$ от максимального возможного количества очков, которые он может набрать, то ему присваивается разряд. Какое наибольшее количество участников турнира могут получить разряд?
комментарий/решение(1)

Задача №3. Обозначим через

$S_n$ — количество упорядоченных наборов из

$n$ натуральных чисел

$(a_1, a_2, . . . , a_n)$ для которых

$\displaylines{\frac{1}{a_1}+\frac{1}{a_2}+. . . +\frac{1}{a_n}=1.}$ Определите четность числа

$S_7$ .
комментарий/решение

Задача №4. Для положительных чисел

$a$ ,

$b$ и

$c$ выполнено равенство

$abc=1$ . Докажите, что

$\displaylines{\frac{1}{a(b+c)}+\frac{1}{b(c+a)}+\frac{1}{c(a+b)} \leq \frac{a+b+c}{2}.}$
комментарий/решение(8)

Задача №5. Дан остроугольный треугольник

$ABC$ , в котором

$AC < AB$ . Его высоты

$BB_1$ и

$CC_1$ пересекаются в точке

$H$ , а прямые

$B_1C_1$ и

$BC$ пересекаются в точке

$P$ . Пусть

$M$ — середина

$BC$ , прямые

$MH$ и

$AP$ пересекается в точке

$K$ . Докажите, что

$KM$ — биссектриса

$\angle B_1KB$ .
комментарий/решение(9)

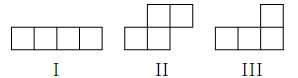
Задача №6. Можно ли клетчатый квадрат размером

$10\times10$ разрезать по линиям сетки на:
а) 4 фигурки вида I и 21 фигурку вида II?
б) 4 фигурки вида I, 19 фигурок вида II и 2 фигурки вида III?
(Фигурки можно произвольно поворачивать и переворачивать)

комментарий/решение(1)