Математикадан республикалық олимпиада, 2008-2009 оқу жылы, 9 сынып

Есеп №1.

$ABC$ үшбұрышында іштей сызылған шеңбер

$BC$ ,

$CA$ және

$AB$ қабырғаларын сәйкесінше

$A_1$ ,

$B_1$ және

$C_1$ нүктелерінде жанап өтеді.

$AC_1B_1$ және

$CA_1B_1$ үшбұрыштарының ортоцентрлерін сәйкесінше

$H_1$ және

$H_2$ арқылы белгілесек, онда

$AH_1H_2C$ төртбұрышына сырттай шеңбер сызуға болатынын дәлелдеңіз.
комментарий/решение(4)

Есеп №2. Шахмат турнирінде 11 адам ойнайды. Турнир барысында әрбір ойыншы басқа әрбір ойыншымен дәл бір партия ойнауы тиіс. Әрбір партия үшін ұтқан адамға 1 ұпай, тең ойнаған адамға

$0,\!5$ ұпай, ал ұтылған адамға 0 ұпай беріледі. Егер турнир аяқталған соң ойыншы максимал мүмкін ұпай санының

$75\%$ -нан кем емес ұпай санын жинаса, оған дәреже беріледі. Ең көп дегенде неше ойыншыға дәреже берілуі мүмкін?
комментарий/решение(1)

Есеп №3.

${{S}_{n}}$ арқылы

$\dfrac{1}{{{a}_{1}}}+\dfrac{1}{{{a}_{2}}}+\ldots +\dfrac{1}{{{a}_{n}}}=1$ теңдігін қанағаттандыратын

$n$ натурал санның

$({{a}_{1}},\,{{a}_{2}},\ldots ,\,{{a}_{n}})$ реттелген қатарларының жалпы санын белгілейік.

${{S}_{7}}$ санының жұптығын анықта.
комментарий/решение

Есеп №4. Оң

$a$ ,

$b$ және

$c$ сандары үшін

$abc=1$ теңдігі орындалатыны белгілі болса, келесі теңсіздікті дәлелде:

$\dfrac{1}{a(b+c)}+\dfrac{1}{b(c+a)}+\dfrac{1}{c(a+b)}\le \dfrac{a+b+c}{2}.$
комментарий/решение(8)

Есеп №5. Сүйірбұрышты

$ABC$ үшбұрышында

$AB < AC$ , оның

$BB_1$ және

$CC_1$ биіктіктері

$H$ нүктесінде, ал

$B_1C_1$ және

$BC$ түзулері

$P$ нүктесінде қиылысады,

$M$ —

$BC$ қабырғасының ортасы.

$MH$ және

$AP$ түзулері

$K$ нүктесінде қиылысатыны белгілі болса,

$KM$ түзуі

$\angle {{B}_{1}}KB$ бұрышының биссектрисасы болатынын дәлелде.
комментарий/решение(9)

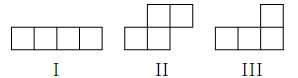
Есеп №6. Бірлік клеткаларға бөлінген

$10\times 10$ шаршыны клетка қабығаларының бойымен:
а) I түрдегі 4 фигураға және II түрдегі 21 фигураға;
ә) I түрдегі 4 фигураға, II түрдегі 19 фигураға және III түрдегі 2 фигураға бөлуге бола ма?
(Фигураларды еркін бұруға және төңкеруге болады).

комментарий/решение(1)