8-я олимпиада им. Шалтая Смагулова, 6-7 класс, 3 (командный) тур

Задача №1. Дана таблица размера $9\times 9$. Каждая клетка закрашена в чёрный или белый цвет. Разрешено выполнять следующую операцию: перекрасить все клетки некоторой строки или столбца в тот цвет, который преобладает в этой строке или столбце (то есть цвет большинства). Всегда ли можно с помощью таких операций перекрасить всю таблицу в один цвет?
комментарий/решение

Задача №2. Числа 1, 2, $\ldots$, 99 разделены на $n$ групп таким образом, что выполнены два условия:
   1) каждое число входит ровно в одну из группу;
   2) если два числа входят в одну группу, то их сумма не кратна 3.
   Найдите наименьшее возможное значение $n$.
комментарий/решение

Задача №3. Изначально комнате находились 7 человек, каждый из которых либо рыцарь, либо лжец. Четыре человека по очереди начали уходить из комнаты, и перед уходом каждый сказал: «После моего ухода лжецов в комнате останется больше, чем рыцарей». Сколько лжецов было в комнате изначально? (Рыцари говорят только правду, а лжецы — только ложь.)
комментарий/решение

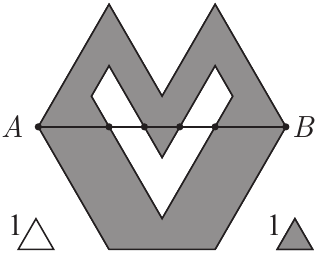
Задача №4. Даны несколько единичных треугольников (то есть каждая сторона каждого треугольника равна 1) двух цветов: серого и белого. Соединяя эти треугольники по стороне составили фигуру на рисунке. Длина отрезка $AB$, соединяющего две точки фигуры, равна 7, и делится серой и белой частями на отрезки длин 2 и 1. Чему равно отношение площади белой части фигуры к площади серой части? (На рисунке масштаб полностью соблюдён, а два треугольника слева и справа от фигуры даны для наглядности.)

комментарий/решение

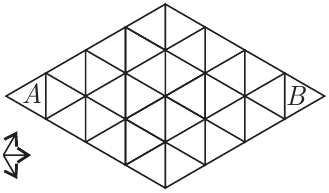
Задача №5. На рисунке из треугольника $A$ нужно добраться до треугольника $B$, двигаясь по указанным стрелкам, переходя из треугольника в соседний треугольник по стороне. Сколькими способами можно это сделать?

комментарий/решение

Задача №6. Существует ли набор из 4 различных натуральных чисел такой, что произведение любых двух чисел из набора делится на их сумму?
комментарий/решение

Задача №7. Дан треугольник $ABC$. Точки $D$, $E$ и $F$ выбраны соответственно на сторонах $AB$, $BC$ и $CA$ так, что $DE = EF = FD$. Известно, что $\angle DEB = \frac{\angle ADF + \angle CFE}{2}$. Докажите равенство $AB = AC$.
комментарий/решение

Задача №8. Анвар покрасил каждую точку плоскости в красный или синий цвет. Арлан хочет найти равнобедренный треугольник у которого одна из сторон равна 1 и все его вершины одного цвета. Всегда ли он сможет такое сделать?
комментарий/решение

Задача №9. Олимпиаду писали несколько учеников. Тренер не помнит, сколько было учеников и кто сколько задач решил. Но он помнит, что любой ученик решил:
   1) больше, чем одну пятую от того, что решили остальные;
   2) и меньше, чем одну треть от того, что решили остальные.
   Сколько учеников могли писать эту олимпиаду?
комментарий/решение

Задача №10. В выпуклом четырёхугольнике $ABCD$ известно, что $BC + DC = AC$, $\angle BCD = 120^\circ$ и диагональ $AC$ является биссектрисой угла при вершине $C$. Докажите, что $AB = AD$.
комментарий/решение(1)

Задача №11. Существует ли такое натуральное число $A$, что при записывании чисел $A, A^2, A^3$ друг за другом получится десятизначное число, содержащее все цифры от 0 до 9?
комментарий/решение

Задача №12. Вычислите: $\frac{1^2}{1^2-1 \cdot 40+800}+\frac{2^2}{2^2-2 \cdot 40+800}+\frac{3^2}{3^2-3 \cdot 40+800}+\cdots+\frac{39^2}{39^2-39 \cdot 40+800}.$
комментарий/решение(1)

Задача №13. Найдите наибольшее значение выражения: $|2x-y|+|2y-z|+|2z-x|$, где $0 \le x,y,z \le 1$.
комментарий/решение

Задача №14. В городе имеется $n$ $(n \ge 5)$ линий метро, и на одной станции пересекаются не более 3 линий метро. Известно, что для любых двух линий существует третья линия, которая с ними пересекается. Докажите, что в этом городе станций метро не меньше $\frac{5}{6}(n-5)$.
комментарий/решение

Задача №15. Найдите наименьшее натуральное число $n$, для которого выполнено условие: если $p$ — простое число и $n$ делится на $p-1$, то $n$ делится на $p$.
комментарий/решение(1)

Задача №16. Верно ли, что для любого целого $n \ge 2$ существуют $n$ различных целых чисел таких, что сумма любых двух из них делится на их разность?
комментарий/решение