8-я олимпиада им. Шалтая Смагулова, 6-7 класс, 3 (командный) тур

Есеп №1. $9 \times 9$ өлшемді кесте берілген. Әр ұяшық қара немесе ақ түске боялған. Кестеге келесі әрекет жасауға рұқсат етіледі: кейбір жолды немесе бағанды сол жолда немесе бағанда ең көп кездесетін түске бояуға болады. Осындай әрекеттермен кестенің барлық ұяшықтарын бір түске бояу әрқашан мүмкін бе?
комментарий/решение

Есеп №2. Келесі екі шарт орындалатындай 1, 2, $\ldots$, 99 сандары $n$ топқа бөлінген:
   1) әр сан дәл бір топқа кіреді;
   2) егер екі сан бір топқа кірсе, онда олардың қосындысы 3-ке бөлінбейді.
   $n$-нің ең кіші мүмкін мәнін табыңыз.
комментарий/решение

Есеп №3. Бөлмеде бастапқыда 7 адам болған, әр адам не сері, не өтірікші. Төрт адам бөлмеден бірінен соң бірі шығып, әрқайсысы кетер алдында: «Мен шыққаннан кейін бөлмеде өтірікшілер серілерден көп болады» -- деді. Бастапқыда бөлмеде неше өтірікші болған? (Серілер тек шындықты айтады, ал өтірікшілер тек өтірік айтады.)
комментарий/решение

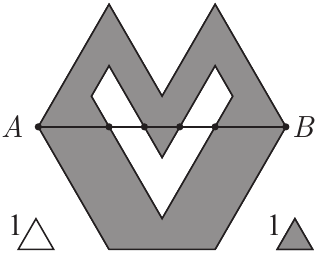
Есеп №4. Әр қабырғасы 1-ге тең бірнеше бірлік үшбұрыш берілген. Олардың түсі — сұр немесе ақ. Осы үшбұрыштарды қабырғалары бойынша біріктіріп, суретте көрсетілген фигура алынған. $AB$ кесіндісінің ұзындығы 7-ге тең, ол сұр және ақ бөліктермен ұзындығы 2 және 1 болатын кесінділерге бөлінген. Фигурадағы ақ бөліктің ауданының сұр бөліктің ауданына қатынасын табыңыз. (Суретте масштаб сақталған, сол және оң жақтағы үшбұрыштар тек көрнекілік үшін салынған.)

комментарий/решение

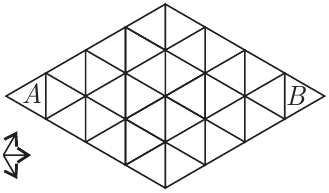
Есеп №5. Суретте $A$ үшбұрышынан $B$ үшбұрышына дейін неше түрлі жолмен жете аламыз? Бір үшбұрыштан оған қабырға бойынша көрші үшбұрышқа ғана өтуге және көрсетілген бағыттардың бірімен ғана жүруге рұқсат.

комментарий/решение

Есеп №6. Кез келген екеуінің көбейтіндісі сол екеуінің қосындысына бөлінетіндей 4 әртүрлі натурал сан табылады ма?
комментарий/решение

Есеп №7. $ABC$ үшбұрышы берілген. $D$, $E$, $F$ нүктелері, сәйкесінше, $AB$, $BC$, $CA$ қабырғаларынан $DE=EF=FD$ болатындай алынған. Егер $\angle DEB=\frac{\angle ADF+\angle CFE}{2}$ болса, онда $AB=AC$ екенін дәлелдеңіз.
комментарий/решение

Есеп №8. Ануар жазықтықтағы әр нүктені қызыл немесе көк түске бояды. Арлан бір қабырғасының ұзындығы 1-ге тең және барлық төбесі бір түсті болатын тең бүйірлі үшбұрыш тапқысы келеді. Арлан өз дегеніне әрқашан да жете ала ма?
комментарий/решение

Есеп №9. Олимпиаданы бірнеше оқушы жазған. Тренер қанша оқушы болғанын және кім қанша есеп шешкенін есінде сақтамаған. Бірақ ол мынаны біледі: әр оқушы қалған оқушылар шешкен есептердің
   1) бестен бірінен артық
   2) және үштен бірінен кем
   есеп шешкен. Олимпиаданы қанша оқушы жазуы мүмкін?
комментарий/решение

Есеп №10. Дөңес $ABCD$ төртбұрышында $BC+DC=AC$, $\angle BCD=120^\circ$ және $AC$ диагоналі $C$ бұрышының биссекрисасы екені белгілі. $AB=AD$ екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №11. $A$, $A^2$, $A^3$ сандарын бірінен кейін бірін тіркеп жазғанда, 10 таңбалы сан шығатындай әрі сол санда 0-ден 9-ға дейінгі цифрлар дәл бір реттен кездесетіндей натурал $A$ саны табыла ма?
комментарий/решение

Есеп №12. Есептеңіз: $\frac{1^2}{1^2 - 1 \cdot 40 + 800} + \frac{2^2}{2^2 - 2 \cdot 40 + 800} + \frac{3^2}{3^2 - 3 \cdot 40 + 800} + \cdots + \frac{39^2}{39^2 - 39 \cdot 40 + 800}.$
комментарий/решение(1)

Есеп №13. $0 \le x, y, z \le 1$ сандары үшін $|2x - y| + |2y - z| + |2z - x|$ өрнегінің ең үлкен мәнін табыңыз.
комментарий/решение

Есеп №14. Бір қалада $n$ $(n \ge 5)$ метро желісі бар және бір станцияда ең көп дегенде 3 метро желісі қиылысады. Метроның кез келген екі желісін байланыстыратын үшінші желі бар екені белгілі. Осы қалада кем дегенде $\frac{5}{6}(n-5)$ метро станциясы бар екенін дәлелдеңіз.
комментарий/решение

Есеп №15. Егер $p$ жай сан болса және $n$ саны $p-1$ санына бөлінсе, онда $n$ саны $p$ санына да бөлінетіндей ең кіші натурал $n$ санын табыңыз.
комментарий/решение(1)

Есеп №16. «Кез келген бүтін $n \ge 2$ саны үшін, кез келген екеуінің қосындысы олардың айырымасына бөлінетіндей $n$ әртүрлі бүтін табылады» деген тұжырым дұрыс па?
комментарий/решение