11-я международная Иранская олимпиада по геометрии, 2024 год, вторая лига, 9-10 классы

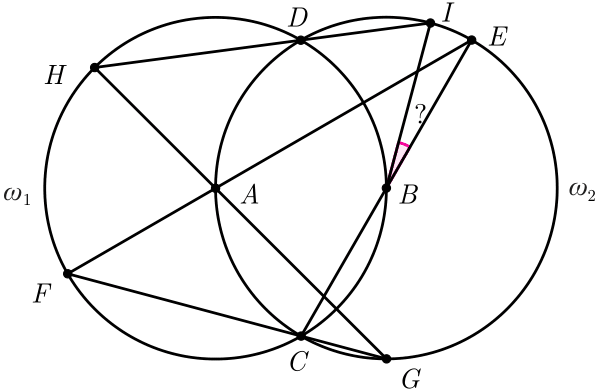
Есеп №1. Төмендегі суретте

$A$ және

$B$ нүктелері

$\omega_1$ және

$\omega_2$ шеңберлерінің центрлері болып келеді.

$BC$ түзуінен бастап

$E, F, G, H, I$ нүктелері кезек-кезекпен алынады.

$IBE$ бұрышын табыңыз.

комментарий/решение(1)

Есеп №2. Дөңес

$ABCDE$ бесбұрышының

$CD$ қабырғасынан

$X$ және

$Y$ нүктелері алынған (

$X$ нүктесі

$Y$ пен

$C$ арасында жатыр).

$\triangle XCB$ ,

$\triangle ABX$ ,

$\triangle AXY$ ,

$\triangle AYE$ және

$\triangle YED$ үшбұрыштары бір біріне ұқсас болсын (сәйкес төбелер дәл осы төбелер ретімен есептелінген).

$ACD$ және

$AXY$ үшбұрыштарына сырттай сызылған шеңберлердің жанасатынын дәлелдеңіз.
комментарий/решение(4)

Есеп №3. Сүйірбұрышты

$ABC$ үшбұрышының

$BC$ қабырғасынан

$D$ нүктесі белгіленген.

$AC$ қабырғасынан

$\angle BAD = 2\angle ADJ$ болатындай

$J$ нүктесі белгіленген.

$\omega$ арқылы

$\triangle CDJ$ -ға сырттай сызылған шеңберді белгілейік.

$AD$ түзуі

$\omega$ -ны екінші рет

$P$ нүктесінде қисын.

$Q$ арқылы

$J$ нүктесінен

$AB$ -ға түсірілген перпендикуляр табанын белгілейік. Егер

$JP = JQ$ болса, онда

$A$ нүктесінен

$DJ$ түзуіне жүргізілген перпендикуляр түзу

$\omega$ -ны жанайтынын дәлелдеңіз.
комментарий/решение

Есеп №4. Эрик бірнеше орталық симметриялы плиткалардан дөңес

$P$ көпбұрышын құрастырды (плиткалар тең болуы және дөңес болуы міндетті емес).

$P$ көпбұрышы да центрлік симметриялы фигура екенін дәлелдеңіз.
комментарий/решение

Есеп №5.

$AB \parallel CD$ болатын

$ABCD$ трапециясының

$AC$ және

$BD$ диагоналдары

$P$ нүктесінде қиылысады.

$\omega_1$ және

$\omega_2$ арқылы, сәйкесінше,

$\triangle APD$ және

$\triangle BPC$ -ға сырттай сызылған шеңберлерді белгілейік.

$AD$ түзуіне

$PDC$ бұрышының ішкі биссектрисасына қатысты симметриялы түзу

$\omega_1$ -ді

$D'$ нүктесінде,

$BC$ түзуіне

$PCD$ бұрышының ішкі биссектрисасына қатысты симметриялы түзу

$\omega_2$ -ні

$C'$ нүктесінде қияды.

$C'A$ түзуі

$\omega_2$ -ні екінші рет

$Y$ нүктесінде, ал

$D'C$ түзуі

$\omega_1$ -ді екінші рет

$X$ нүктесінде қисын.

$P, X, Y$ нүктелері бір түзудің бойында жатқанын дәлелдеңіз.
комментарий/решение