11-я международная Иранская олимпиада по геометрии, 2024 год, вторая лига, 9-10 классы

На рисунке ниже точки $A$ и $B$ — это центры окружностей $\omega_1$ и $\omega_2$. Начиная с прямой $BC$, точки $E, F, G, H, I$ получены последовательно. Найдите угол $\angle IBE$.

Комментарий/решение

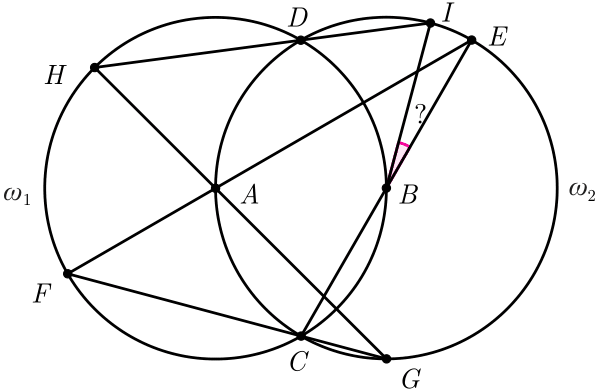
Oтвет:$\angle IBE = 15^\circ$

Так как окружностим равны, значить $\square ABCD$ ромб где один угол равен $60^\circ$ $\Leftrightarrow \angle ADB = \angle ABC = \angle BCA = \angle CAB = \angle BDE = 60^\circ$. $BA$ и $BE$ радиусы значить $ \angle BAE = \angle BEA = 30^\circ$ $\Rightarrow \angle CAE = 90^\circ$ $\Rightarrow \angle AFC = \angle ACF = 45^\circ$ $\Rightarrow \angle ECG = 75^\circ$. $\angle CEA = \angle CGA = 30^\circ$ т.к. они смторит дугу $CA$. Значить $ \angle CAG = 180^\circ - \angle ACG - \angle CGA = 15^\circ \Rightarrow \angle GAB = 45^\circ \Rightarrow DAH = 180^\circ - \angle GAD = 75^\circ$ $AH$ и $AD$ радиусы значить $\angle AHD = \angle ADH = 52.5^\circ \Rightarrow \angle BDI = 180^\circ - \angle BDH =67.5^\circ$ $BD$ и $BI$ радиусы значить $\angle DBI = 180^\circ - \angle BDI - \angle BID = 45^\circ \Rightarrow \angle IBE = 60^\circ - \angle DBI = 15^\circ$

Пусть $K$ симметричная точке $E$ относительно $BI$, тогда $\angle KBG=\angle EBK+\angle EBG=180-2\angle CEK+180-\angle GBC=180\longrightarrow \angle IBE=\dfrac{\angle KBE}{2}=\dfrac{\angle CBG}{2}=\angle CAG=15^\circ$