11-я международная Иранская олимпиада по геометрии, 2024 год, вторая лига, 9-10 классы

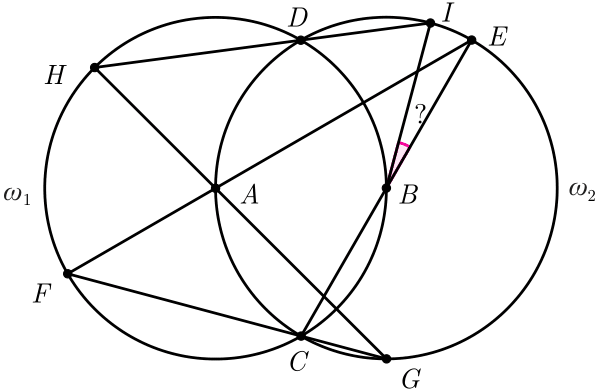
Задача №1. На рисунке ниже точки $A$ и $B$ — это центры окружностей $\omega_1$ и $\omega_2$. Начиная с прямой $BC$, точки $E, F, G, H, I$ получены последовательно. Найдите угол $\angle IBE$.

комментарий/решение

Задача №2. Точки $X$ и $Y$ лежат на стороне $CD$ выпуклого пятиугольника $ABCDE$ ($X$ находится между $Y$ и $C$). Предположим, что треугольники $\triangle XCB$, $\triangle ABX$, $\triangle AXY$, $\triangle AYE$ и $\triangle YED$ все подобны друг другу (в указанном порядке). Докажите, что описанные окружности треугольников $\triangle ACD$ и $\triangle AXY$ касаются.
комментарий/решение(1)

Задача №3. Пусть $ABC$ — остроугольный треугольник, а точка $D$ лежит на стороне $BC$. Пусть $J$ такая точка на стороне $AC$, что $\angle BAD = 2\angle ADJ$. Обозначим через $\omega$ описанную окружность треугольника $CDJ$. Прямая $AD$ пересекает $\omega$ во второй раз в точке $P$, а $Q$ — основание перпендикуляра из точки $J$ на прямую $AB$. Докажите, что если $JP = JQ$, то прямая, перпендикулярная к $DJ$ и проходящая через $A$, касается окружности $\omega$.
комментарий/решение

Задача №4. Эрик собрал выпуклый многоугольник $P$ из конечного числа центрально симметричных (не обязательно равных или выпуклых) многоугольных плиток. Докажите, что $P$ также является центрально симметричным.
комментарий/решение

Задача №5. Диагонали $AC$ и $BD$ трапеции $ABCD$ ($AB \parallel CD$) пересекаются в точке $P$. Обозначим через $\omega_1$ и $\omega_2$ описанные окружности $\triangle APD$ и $\triangle BPC$ соответственно. Отражение прямой $AD$ относительно внутренней биссектрисы $\angle PDC$ пересекает $\omega_1$ в точке $D'$, а отражение прямой $BC$ относительно внутренней биссектрисы $\angle PCD$ пересекает $\omega_2$ в точке $C'$. Прямая $C'A$ во второй раз пересекает $\omega_2$ в точке $Y$, а прямая $D'C$ во второй раз пересекает $\omega_1$ в точке $X$. Докажите, что точки $P, X, Y$ лежат на одной прямой.
комментарий/решение