Международная олимпиада 2023, Чиба, Япония, 2023 год

Задача №1. Найдите все составные натуральные числа

$n>1$ со следующим свойством: если через

$d_1, d_2, \ldots, d_k$ обозначить все натуральные делители числа

$n$ , причем

$1=d_1 < d_2 < \ldots < d_k=n$ , то

$d_i$ делит

$d_{i+1}+d_{i+2}$ для всех

$1 \leqslant i \leqslant k-2$ .
комментарий/решение(6)

Задача №2. Дан остроугольный треугольник

$ABC$ , причем

$AB < AC$ . Окружность

$\Omega$ описана около треугольника

$ABC$ . Середину ее дуги

$CB$ , содержащей точку

$A$ , обозначим через

$S$ . Прямая, проходящая через

$A$ и перпендикулярная стороне

$BC$ , пересекает отрезок

$BS$ в точке

$D$ и пересекает

$\Omega$ второй раз в точке

$E \neq A$ . Прямая, проходящая через

$D$ и параллельная стороне

$BC$ , пересекает прямую

$BE$ в точке

$L$ . Окружность, описанную около треугольника

$BDL$ , обозначим через

$\omega$ . Пусть

$P \neq B$ — вторая точка пересечения

$\omega$ с

$\Omega$ . Докажите, что касательная к окружности

$\omega$ в точке

$P$ пересекает прямую

$BS$ в точке, лежащей на биссектрисе угла

$\angle BAC$ .
комментарий/решение(8)

Задача №3. Дано натуральное число

$k \geqslant 2$ . Найдите все бесконечные последовательности положительных целых чисел

$a_1, a_2, \ldots$ со следующим свойством: существует многочлен

$P$ вида

$P(x)=x^k+c_{k-1} x^{k-1}+\cdots+c_1 x+c_0$ с неотрицательными целыми коэффициентами

$c_0, c_1, \ldots, c_{k-1}$ такой, что

$P\left(a_n\right)=a_{n+1} a_{n+2} \cdots a_{n+k}$ для всех натуральных

$n \geq 1$ .
комментарий/решение(5)

Задача №4. Даны попарно различные положительные действительные числа

$x_1, x_2, \ldots, x_{2023}$ такие, что число

$a_n=\sqrt{\left(x_1+x_2+\cdots+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\right)}$ является целым для всех

$n=1,2, \ldots, 2023$ . Докажите, что

$a_{2023} \geqslant 3034$ .
комментарий/решение(4)

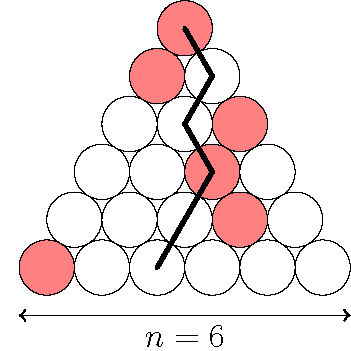
Задача №5. Пусть

$n \geq 1$ натуральное число. Японский треугольник состоит из

$1+2+\cdots+n$ одинаковых кругов, выложенных в форме равностороннего треугольника так, что для каждого

$i=1,2, \ldots, n$ ряд с номером

$i$ состоит ровно из

$i$ кругов, в точности один из которых покрашен в красный цвет. Путем ниндзя в японском треугольнике называется последовательность из

$n$ кругов, построенная следующим образом: начинаем с круга в ряде 1 в затем поочередно спускаемся вниз, переходя от круга к одному из двух кругов непосредственно под ним, пока не дойдем до ряда

$n$ . Ниже приведен пример японского треугольника для

$n=6$ , а также пути ниндзя, содержащего два красных круга. Найдите наибольшее число

$k$ (зависящее от

$n$ ) такое, что в любом японском треугольнике существует путь ниндзя, содержащий хотя бы

$k$ красных кругов.

комментарий/решение(6)

Задача №6. Дан равносторонний треугольник

$ABC$ . Внутри

$ABC$ выбраны точки

$A_1, B_1, C_1$ такие, что

$BA_1=A_1C,$

$CB_1=B_1A,$

$AC_1=C_1B$ и

$\angle BA_1 C+\angle CB_1A+\angle AC_1B=480^{\circ} .$ Прямые

$B C_1$ и

$C B_1$ пересекаются в точке

$A_2$ , прямые

$CA_1$ в

$AC_1$ пересекаются в точке

$B_2$ , прямые

$AB_1$ и

$B A_1$ пересекаются в точке

$C_2$ . Предположим, что у треугольника

$A_1B_1C_1$ стороны имеют попарно различные длины. Докажите, что тогда все три окружности, описанные около треугольников

$A A_1A_2,$

$BB_1B_2$ и

$CC_1C_2$ , проходят через какие-то две общие точки.
комментарий/решение(8)

результаты