Международная олимпиада 2023, Чиба, Япония, 2023 год

$n \geq 1$ натурал сан болсын. Жапон үшбұрышы деп жалпы $1+2+\cdots+n$ бірдей дөңгелектерден құралған, әрбір $i=1,2, \ldots, n$ үшін нөмірі $i$ болатын қатарда дәл $i$ дөңгелегі бар, ал әр қатарда дәл бір дөңгелек қызыл түске боялған тең бүйірлі үшбұрыш түрінде салынған фигураны айтамыз. Жапон үшбұрышындағы ниндзя жолы деп аталатын $n$ дөңгелек тізбегі келесідей құрастырылған: 1-ші қатардағы дөңгелектен бастаймыз, содан кейін кезекпен төменгі бір дөңгелекке түсеміз, сосын оның астындағы екі дөңгелектің біріне жылжи бере, $n$-ші қатарға жету жол. Төменде $n=6$ үшін жапондық үшбұрыштың мысалы, сондай-ақ екі қызыл дөңгелектен тұратын ниндзя жолы берілген. Кез келген жапон үшбұрышында кем дегенде $k$ қызыл дөңгелегі бар ниндзя жолы болатындай ең үлкен $k$ санын ($n$-ға байланысты) табыңыз.

Комментарий/решение

Красивое решение

Уважаемый бекжан

Ваши утверждение полностью неверны и не обоснованны

Например не факт что в любом японсеом триугольнике найдется красный круг под номер лог2 n+1

И вы утверждаете что аналогично можно построить нужный нам японский триугольник хотя это не так. Ваша идея не как не влияет на построение

Согл

Коммент:

Думал ответ $[\frac{n+1}{2}]$- но он не правильный, вот и заблудился. Правильный ответ $[log_2(n)+1]$. Нужно было внимательнее оценить $n=1$,$2$,...,$10$, оттуда у меня выходят две идеи помогающие решить задачу.

Решение:

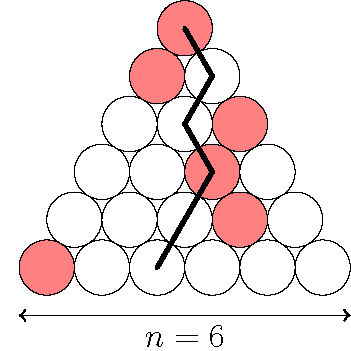
К каждому кругу С отметим число - наибольшее количество красных кругов из всех путей ниндзя проходящие вершину и С. $(!)$ Тогда любое число не меньше предыдущих чисел в любом пути. Пример японского треугольника с числами:

$$\color{red} 1$$

$$\color{red} 2 \quad 1$$

$$2 \quad 2 \quad \color{red} 2$$

$$2 \quad 2 \quad 2 \quad \color{red} 3$$

$(!!)$ Докажем что для $n=2^t-1$ можем покрасить треугольник так что числа в крайнем нижнем ряду равны $t$. Базовый пример для $n=1$, $3$, очевидны. $n=7$:

$$\color{red} 1$$

$$1 \quad \color{red} 2$$

$$\color{red} 2 \quad 2 \quad 2$$

$$2 \quad 2 \quad 2 \quad \color{red} 3$$

$$2 \quad 2 \quad \color{red} 3 \quad 3 \quad 3$$

$$2 \quad \color{red} 3 \quad 3 \quad 3 \quad 3 \quad 3$$

$$\color{red} 3 \quad 3 \quad 3 \quad 3 \quad 3 \quad 3 \quad 3$$

Если верно для $n=2^t-1$, докажем для $n=2^{t+1}-1$.

Выделим треугольник со стороной $2^t-1$ из вершины, его можно покрасить чтобы ряд $2^t-1$ чисел равен $t$. Для $i$-ого ряда снизу красим $i$-ый круг слева в красный. Эти красные круги попарно не имеют общий путь ниндзя, а любой путь проходит через ряд из чисел $t$ и множество красных кругов ниже ровно один раз, из чего крайние нижние числа равны $t+1$.

$$t \quad ... \quad t$$

$$t \quad ... \quad t \quad \color{red} {t+1}$$

$$t \quad ... \quad \color{red} {t+1} \quad t+1 \quad t+1$$

$$t \quad ... \quad \color{red} {t+1} \quad t+1 \quad t+1 \quad t+1 \quad t+1$$

$$\color{red} {t+1} \quad t+1 \quad t+1 \quad ... \quad t+1 \quad t+1 \quad t+1$$

$(!!!)$ Докажем что для $n=2^t$, сумма чисел в крайнем нижнем ряду не меньше $t\cdot 2^t+1$. Базовый пример $n=1,2$ дают $1$,$3$.

Докажем для $n=2^{t+1}$:

$$\color{purple}{s_l} \quad \color{green}{s_m} \quad \color{blue}{s_r}$$

$$...$$

$$\color{purple}{S_l\geq s_l} \quad \color{green}{S_{m_1}\geq s_m} \quad ... \quad \color{green}{S_{m_{2^t+1}}\geq s_m}\quad \color{blue}{S_r\geq s_r}$$

Отметим наибольшее число $\color{green}{s_m}\geq t+1$ в ряду из $2^t$ чисел, а $\color{purple}{s_l}$ и $\color{blue}{s_r}$- суммы подряд идущих чисел слева и справа в том же ряду. Временно стерем красные круги и оценим сумму крайнего нижнего ряда.

В ряду из $2^{t+1}$ чисел существует ровно $2^t+1$ подряд идущих чисел для которых проходит путь ниндзя проходящий $\color{green}{s_m}$. Отметим их как $\color{green}{S_m}$, а $\color{purple}{S_l}$ и $\color{blue}{S_r}$- суммы подряд идущих чисел слева и справа в том же ряду. $(s_l,S_l)$ и $(s_r,S_r)$ можно разбить на лево и право наклоняющеся пути ниндзя соответственно. По $(!)$, $S_m\geq s_m$, $S_l\geq s_l$, $S_r\geq s_r$. Сумма чисел крайнего ряда тогда не меньше:

$$S_l+S_{m_1}+...+S_{m_{2^t+1}}+S_r \geq (s_l+s_m+s_r)+2^t\cdot s_m\geq (t\cdot 2^t+1)+2^t\cdot (t+1)=t\cdot 2^{t+1}+2^t+1$$

Теперь оценим как красные круги влиют на сумму чисел крайнего ряда. Разобьем нижние $2^t$ рядов на лево наклоняющеся диагоналей. Если в диагонале $m$ красных кругов то к сумме крайних нижних чисел добавляется $m$. Так как всего красных кругов в этих диагоналях $2^t$б то сумма крайних нижних чисел хотя бы:

$$(t\cdot 2^{t+1}+2^t+1)+2^t=(t+1)\cdot 2^{t+1}+1$$

Получаем из $(!!)$,$(!!!)$ что для $n=2^t$,...,$2^{t+1}-1$:

$$t+1\leq k\leq t+1$$

Из чего $k=[log_2(n)]+1$.

Ну по моему это легкая задача которую можно решит с одим взглядом и заполучить халявных баллов чтобы вознаграждатся на олимпиаде.

Ответ:нельзя

Решение:разложим 2024 на простые делители.выйдет 2*2*2*11*23.у нас в общем 6 столбцов и строка вместе.каждая клетка является множителем для 2 строк и столбов(1строка и 1 столб).Значит у нас три числа которые делятся на 23.если взять их минимальными то выйдут числа 23;46,92.но при этом в строке или столбце где стоит число 92 будет число делящеесе на 11 а это хотя бы 11.96+11=107.А это уже больше чем 100.