Городская Жаутыковская олимпиада по математике, 6 класс, 2023 год
Задача №1. Айдана сложила квадрат со стороной в 3 спички, как на рисунке, потратив на это 24 спички. Мадина выложила большой квадрат со стороной в 100 спичек. Сколько спичек она потратила?
комментарий/решение(3)

комментарий/решение(3)
Задача №2. Даны четыре одинаковых с виду шара и весы со стрелкой (которые показывают вес груза). Известно, что массы шаров равны 2021 г, 2022 г, 2023 г, 2025 г. Найдите массу каждого шара
а) за 3 взвешивания;
б) за 2 взвешивания.
комментарий/решение(1)
а) за 3 взвешивания;
б) за 2 взвешивания.
комментарий/решение(1)
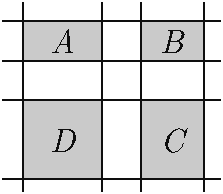
Задача №3. Арман провёл 4 горизонтальных прямых и 4 вертикальных и среди образовавшихся прямоугольников отметил четыре «угловых»: $A$, $B$, $C$ и $D$ (схематично это показано на рисунке). Площади прямоугольников $A$, $D$, $C$ равны 4 см$^2$, 14 см$^2$ и 7 см$^2$ соответственно. Найдите площадь прямоугольника $B$. (Стороны прямоугольников не обязательно целые.)
комментарий/решение(1)
комментарий/решение(1)
Задача №4. Квадрат $7\times 7$ разрезали на части, среди которых не встречается никаких других фигурок, кроме изображённых на рисунке (возможно, повёрнутых или перевёрнутых). Докажите, что в любом таком разрезании встречается ровно одна четырёхклеточная фигурка.
комментарий/решение

комментарий/решение
Задача №5. На доске написано число 1. Два игрока играют в следующую игру, ходя по очереди. За каждый свой ход игрок может стереть число и записать вместо него новое число, которое больше предыдущего на 1, 2 или 3. Выигрывает тот, кто первым получит число 2023. Кто при правильной игре может гарантировать себе победу?
комментарий/решение(1)
комментарий/решение(1)
Задача №6. Числа 1, 2, 3, 4, 5 и 6 записаны по кругу указанном порядке. Каждую минуту все числа одновременно заменяются по следующему правилу: каждое число, за которым следует большее число, увеличивается на 1, каждое число, за которым следует меньшее число, уменьшается на 1, а остальные числа не изменяются. (Все направления считаются по ходу часовой стрелки.) Найдите сумму чисел, записанных по кругу после 2019 минут.
комментарий/решение(1)
комментарий/решение(1)
Задача №7. На доске записано натуральное число. Пете разрешено заменять имеющееся на доске число на сумму квадратов его цифр. Число назовем интересным, если из него за конечное число таких операций Петя не сможет получить единицу. Докажите, что существует бесконечно много интересных натуральных чисел.
комментарий/решение(1)
комментарий/решение(1)
Задача №8. За круглым столом сидят 300 человек: некоторые из них рыцари, а остальные лжецы. Антон спросил у каждого из них: «Сколько лжецов среди твоих соседей?» и сложил полученные числа. Затем Аня сделала то же самое. Отвечая на вопрос, рыцари всегда говорят правду, а лжецы всегда лгут, но называют лишь числа 0, 1 или 2. Оказалось, что сумма чисел у Антона на 400 больше, чем у Ани. Сколько за столом лжецов? Найдите все возможные варианты ответа и докажите, что других нет.
комментарий/решение
комментарий/решение