Городская Жаутыковская олимпиада по математике, 6 класс, 2023 год

Есеп №1. Айдана қабырғасы 3 сіріңкеден тұратын суреттегідей шаршы құрастырды. Оған барлығы 24 сіріңке пайдаланды. Мадина қабырғасы 100 сіріңкеден тұратын үлкен шаршы құрастырды. Ол қанша сіріңке пайдаланды?

комментарий/решение(3)

Есеп №2. Сыртқы пішіндері ұқсас төрт шар және бағыттауыш сызығы бар шардың салмағын көрсететін таразы берілген. Шардың салмақтары 2021 г, 2022 г, 2023 г және 2025 г екені белгілі. Әр шардың салмағы қандай екенін табыңыз.
а) 3 рет өлшеу арқылы;
б) 2 рет өлшеу арқылы.
комментарий/решение(1)

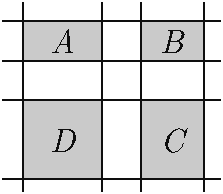
Есеп №3. Арман 4 горизонталь және 4 вертикаль түзу жүргізді. Және олардан «бұрыш» жасап тұрған 4 тіктөртбұрышты $A$, $B$, $C$ және $D$ деп белгіледі (суретке қараңыз). $A$, $D$, $C$ тіктөртбұрыштың аудандары, сәйкесінше, 4 см$^2$, 14 см$^2$ және 7 см$^2$. $B$ тіктөртбұрышының ауданын табыңыз. (Тіктөртбұрыштың қабырғалары бүтін сан болмауы мүмкін.)

комментарий/решение(1)

Есеп №4. Өлшемі $7\times 7$ болатын шаршы берілген. Шаршыны суретте көрсетілген фигураларға бөлген және одан басқа фигура кездеспейді (фигуралар бұрылып тұруы мүмкін). Осындай бөлу кезінде тек бір ғана төрт торкөздік фигура болатынын дәлелдеңіз.

комментарий/решение

Есеп №5. Тақтаға 1 саны жазылған. Екі ойыншы кезектесе жүре отыра келесі ойынды ойнайды. Әр ойыншы өзінің жүрісінде тақтадағы санды өшіріп, оның орнына өшірген саннан 1, 2 немесе 3-ке артық санды жаза алады. Бірінші болып 2023 санын алған ойыншы жеңеді. Дұрыс ойында қай ойыншы жеңеді: ойынды бастаған ойыншы ма әлде оның қарсыласы ма?
комментарий/решение(1)

Есеп №6. 1, 2, 3, 4, 5 және 6 сандары шеңбер осы көрсетілген ретпен жазылады. Әр минут сайын барлық сандар бір уақытта келесі ереже бойынша ауыстырылады: егер қандай да бір саннан кейін одан үлкен сан тұрса, онда сол қандай да бір сан 1-ге артылады, егер қандай да бір саннан кейін сол саннан кіші сан тұрса, онда сол қандай да бір сан 1-ге азайтылады, ал қалған жағдайда сандар өзгермейді. (Барлық бағыт сағат тілімен есептеледі.) 2019 минуттан кейін шеңберге жазылған сандардың қосындысын табыңыз.
комментарий/решение(1)

Есеп №7. Тақтада натурал сан жазылған. Петяға тақтадағы санды оның цифрларының квадраттарының қосындысына ауыстыруға рұқсат етіледі. Петя осындай операциялардың шекті санында сол тақтадағы саннан 1 санын ала алмаса, ондай санды қызықты сан деп атаймыз. Қызықты натурал сандардың саны шексіз көп екенін дәлелдеңдер.
комментарий/решение(1)

Есеп №8. Дөңгелек үстел бойында 300 адам отыр: олардың кейбіреулері серілер, ал қалғандары өтірікшілер. Антон олардың әрқайсысынан: «Көршілеріңіздің қаншасы өтірікші?» деп сұрап, жауап ретінде алған сандарды қосты. Содан кейін Аня да солай істеді. Сұраққа жауап бергенде серілер әрқашан шындықты айтады, ал өтірікшілер әрқашан өтірік айтады, бірақ өтірікшілер жауап ретінде тек 0, 1 немесе 2 сандарын береді. Антонның сандарының қосындысы Аняның қосындысынан 400-ге артық болып шықты. Үстел басында қанша өтірікші отыр? Барлық мүмкін жауаптарды табыңыз және одан басқа жауап жоқ екенін дәлелдеңіз.
комментарий/решение