Городская Жаутыковская олимпиада по математике, 6 класс, 2022 год

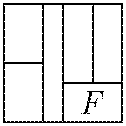
Задача №1. Квадрат разрезан на шесть прямоугольников так, как показано на рисунке. Оказалось, что площади всех прямоугольников равны. Найдите отношение сторон прямоугольника, отмеченного буквой $F$.

комментарий/решение

Задача №2. Найдите семь решений ребуса: $FIZ\cdot MAT=50 \cdot LET.$ (Разным цифрам соответствуют разные буквы и наоборот.)
комментарий/решение(1)

Задача №3. Числа от 1 до 2022 разбили на две группы по 1011 чисел. Затем числа в группах перемножили. Могло ли оказаться так, что разность этих двух произведении равняется 2121?
комментарий/решение(1)

Задача №4. На уроке физкультуры выстроились в ряд 15 мальчиков и 15 девочек. Каждый из 30 детей держал в руках у мячику. Учитель велел каждому мальчику передать свой мяч соседу справа, а каждый девочке — соседу слева. При этом половина детей выполнила команду правильно, а остальные перепутали и отдали мяч соседу с другой стороны. Докажите что кто-то остался без мяча.
комментарий/решение

Задача №5. На экране высвечено число 48. При нажатии кнопки все цифры числа перемножаются, к результату прибавляется 27, полученное число высвечивается на экране (предыдущее число стирается). Кнопку нажали 2022 раза. Какое число теперь на экране?
комментарий/решение

Задача №6. Разрежьте клетчатый квадрат $6 \times 6$ на «трёхклетчатые» уголки

и прямоугольники $1\times 3$

так, чтобы каждая фигура граничила (имела общий отрезок) с фигурками обоих типов. (Фигурки можно поворачивать и переворачивать.)
комментарий/решение

Задача №7. а) Можно ли выписать на доске четыре различных двузначных чисел так, чтобы разность любых двух из них было простым числом?
б) Можно ли выписать на доске пять различных двузначных чисел так, чтобы разность любых двух из них было простым числом?
комментарий/решение(1)

Задача №8. В классе было 20 учеников. После уроков, за плодотворную работу учеников, учитель начал вручать каждому ученику ровно по одной конфетке. Но конфеток хватило не всем. Тогда учитель решил сбегать в магазин за конфетками, и покинул временно кабинет. Время от времени один из учеников давал свою конфетку другому ученику, у которого не было конфетки. В конце 10 учеников подсчитали, что каждый из них отдавал конфетку больше, чем получал. Скольким ученикам учитель успел раздать конфетки перед тем, как уйти в магазин?
комментарий/решение