Республиканская олимпиада по физике 2013, 11 класс, теоретический тур
Задача №1. (10,0 балла)
Тело может двигаться по внутренней поверхности параболоида вращения, сечение которого имеет уравнение $z=kr^2$. Тело, находящееся на высоте $z_0$ от вершины, начинает двигаться вдоль поверхности с горизонтальной скоростью $\vartheta_0$. Ускорение свободного падения равно $g$, геометрические размеры тела очень малы.
а) При определенном значении горизонтальной скорости $\vartheta_0$, которое обозначим $\vartheta_{h}$, тело двигается по горизонтальной окружности. Найдите $\vartheta_{h}$;
б) Пусть теперь $\vartheta_0>\vartheta_h$. На какую максимальную высоту $z_{\max}$ поднимется тело?
Пусть теперь $\vartheta_0=0$.
в) Считая $z_0$ малым, найдите период колебаний тела;
г) Пусть $z_0$ произвольно. Будет ли период движения большим или меньшим по сравнению с вычисленным в пункте в)? Ответ обоснуйте.
комментарий/решение
Тело может двигаться по внутренней поверхности параболоида вращения, сечение которого имеет уравнение $z=kr^2$. Тело, находящееся на высоте $z_0$ от вершины, начинает двигаться вдоль поверхности с горизонтальной скоростью $\vartheta_0$. Ускорение свободного падения равно $g$, геометрические размеры тела очень малы.
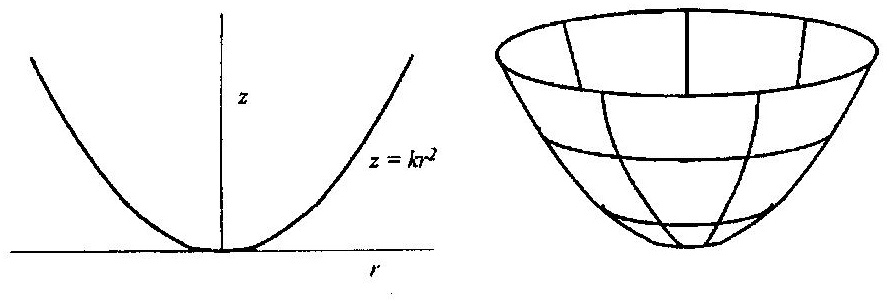
а) При определенном значении горизонтальной скорости $\vartheta_0$, которое обозначим $\vartheta_{h}$, тело двигается по горизонтальной окружности. Найдите $\vartheta_{h}$;
б) Пусть теперь $\vartheta_0>\vartheta_h$. На какую максимальную высоту $z_{\max}$ поднимется тело?
Пусть теперь $\vartheta_0=0$.
в) Считая $z_0$ малым, найдите период колебаний тела;
г) Пусть $z_0$ произвольно. Будет ли период движения большим или меньшим по сравнению с вычисленным в пункте в)? Ответ обоснуйте.
комментарий/решение
Задача №2. (7.0 балла)
Рассмотрим явление звуковой люминесценции. Пусть в жидкости в состоянии равновесия находится пузырек с газом. Распространяющаяся в газе звуковая волна сжимает пузырек настолько, что температура газа становится достаточной для излучения света. На самом деле пузырек претерпевает целую серию сжатий и расширений, вызываемых изменением давления в звуковой волне. В дальнейшем будем работать с простейшей моделью звуковой люминесценции. Предположим, что первоначальное давление газа внутри пузырька равно атмосферному $P_0=100$ кПа. Когда давление в жидкости, окружающей пузырек, уменьшается, пузырек расширяется изотермически до радиуса $r_{\max}=36.0$ мкм. Когда давление звуковой волны нарастает, пузырек сжимается до радиуса $r_{\min}=4,50$ мкм настолько быстро, что газ внутри пузырька не успевает обмениваться теплом с окружающей средой. Между сжатием и расширением пузырек изохорически (при постоянном объеме) остывает до начального давления и температуры окружающей среды. Пусть пузырек, содержащий одноатомный идеальный газ, находится в воде, имеющей температуру $T_0= 293$ К. Универсальная газовая постоянная равна $R=8.31$ Дж/( моль $\cdot$ K).
комментарий/решение
Рассмотрим явление звуковой люминесценции. Пусть в жидкости в состоянии равновесия находится пузырек с газом. Распространяющаяся в газе звуковая волна сжимает пузырек настолько, что температура газа становится достаточной для излучения света. На самом деле пузырек претерпевает целую серию сжатий и расширений, вызываемых изменением давления в звуковой волне. В дальнейшем будем работать с простейшей моделью звуковой люминесценции. Предположим, что первоначальное давление газа внутри пузырька равно атмосферному $P_0=100$ кПа. Когда давление в жидкости, окружающей пузырек, уменьшается, пузырек расширяется изотермически до радиуса $r_{\max}=36.0$ мкм. Когда давление звуковой волны нарастает, пузырек сжимается до радиуса $r_{\min}=4,50$ мкм настолько быстро, что газ внутри пузырька не успевает обмениваться теплом с окружающей средой. Между сжатием и расширением пузырек изохорически (при постоянном объеме) остывает до начального давления и температуры окружающей среды. Пусть пузырек, содержащий одноатомный идеальный газ, находится в воде, имеющей температуру $T_0= 293$ К. Универсальная газовая постоянная равна $R=8.31$ Дж/( моль $\cdot$ K).
- Сколько молей газа $\nu$ содержится внутри одного пузырька?
- Чему равно давление газа $P_1$ в пузырьке после расширения?
- Чему равно давление газа $P_2$ в пузырьке после его сжатия?
- Чему равна температура газа $T_2$ в пузырьке после сжатия?
- Чему равна работа $A$, совершаемая над пузырьком за время одного цикла сжатия и расширения?
комментарий/решение
Задача №3. (8.0 балла)
С помощью кабеля питания высоковольтной линии передается электрический ток синусоидальной формы частотой $\nu=60$ Гц. Нагрузка работает при действующем значении напряжения $U_0=500$ кВ и потребляет мощность $P=1000$ МВт. В данной задаче рассматривайте только электрический ток, текущий в одном из двух возможных направлений и полностью пренебрегайте емкостью и индуктивностью между кабелем и землей. Магнитная постоянная равна $\mu_0=4\pi\times10^{-7}$ Гн/м. Предположим, что нагрузка представляет собой группу зданий, которые можно рассматривать как обычное сопротивление.
комментарий/решение
С помощью кабеля питания высоковольтной линии передается электрический ток синусоидальной формы частотой $\nu=60$ Гц. Нагрузка работает при действующем значении напряжения $U_0=500$ кВ и потребляет мощность $P=1000$ МВт. В данной задаче рассматривайте только электрический ток, текущий в одном из двух возможных направлений и полностью пренебрегайте емкостью и индуктивностью между кабелем и землей. Магнитная постоянная равна $\mu_0=4\pi\times10^{-7}$ Гн/м. Предположим, что нагрузка представляет собой группу зданий, которые можно рассматривать как обычное сопротивление.
- Каково действующее значение электрического тока $I$ в кабеле питания высоковольтной линии передач?
- Кабель, имеющий диаметр $d=3$ см и длину $l=500$ км, изготовлен из алюминия с удельным сопротивлением $\rho=2.8\times10^{-8}$ Ом $\cdot$ м. Какая мощность $P_0$ теряется в кабеле питания высоковольтной линии передач?
- Найдите аналитическое выражение для э.д.с. индукции, наводимой в контуре кабелем;
- Пусть $a=5$ м, $b=2$ м и $h=100$ м. Сколько витков $N$ должен содержать контур для того, чтобы в нем индуцировалась действующее значение э.д.с., равное $\varepsilon_{\sigma}=120$ В?
- Возросла ли мощность, теряемая в кабеле питания? Ответ обоснуйте;
- Энергетическая компания, которой принадлежат сети, решила сделать ситуацию, какой она была до подключения завода. Для этого они параллельно заводу подключили конденсатор. Какова его емкость $C$?
Продвинутый фермер, живущий вблизи линии передач, подумал, что он сможет извлечь из кабеля электрическую энергию, используя явление электромагнитной индукции. Фермер изготовил прямоугольный контур длины $a$ и ширины $b
В качестве нагрузки к группе зданий подключается завод, на котором работает большое количество электродвигателей. Оказалась, что потребляемая мощность не изменилась, а сам завод можно рассматривать как катушку индуктивности $L=0,25$ Гн, подключенную параллельно к группе зданий.
комментарий/решение
Задача №4. (5.0 балла)
В данной задаче рассматривается упрощенная модель электромагнитного излучения, запертого внутри куба со стороной $L$. Электрическое поле внутри куба имеет пространственную зависимость $E(x,y,z)=E_0\sin(k_{x}x)\sin(k_{y}y)\sin(k_{z}z)$, при этом считается, что одна из вершин куба находится в начале координат, а стороны куба направлены вдоль осей $x,y$ и $z$ соответственно. Пусть $h$ — постоянная Планка, $k_{B}$ — постоянная Больцмана, $c$ — скорость света.
а) Электрическое поле должно быть равно нулю на всех гранях куба. Каковы возможные значения $k_{x},k_{y}$ и $k_{z}$?
б) В этой модели каждому возможному набору значений $(k_{x},k_{y}$,$k_{z})$ соответствует одно так называемое квантовое состояние. Все возможные квантовые состояния могут быть изображены точками в так называемом пространстве состояний, представляющем собой воображаемое пространство с введенными декартовыми координатами $k_{x},k_{y}$ и $k_{z}$. Сколько состояний $N$ находится в некотором объеме $s$ пространства состояний? $s$ настолько велико, что дискретностью квантовых состояний можно пренебречь;
в) Каждому квантовому состоянию может соответствовать фотон с частотой $\omega=c|k|$, где $|k|=\sqrt{k_{x}^2+k_{y}^2+k_{z}^2}$. Пусть температура системы равна $T$. Известно, что ни один фотон не может иметь энергию, большую чем $k_{B}T$. Определите форму и размеры области в пространстве состояний, которая может быть занята фотонами;
г) Пусть каждое возможное квантовое состояние занято одним фотоном. Найдите полную энергию всех фотонов в кубе. Считайте, что температура настолько высока, что внутри куба находится очень большое число квантовых состояний. Подсказка: надо разделить пространство состояний на сферические слои.
комментарий/решение
В данной задаче рассматривается упрощенная модель электромагнитного излучения, запертого внутри куба со стороной $L$. Электрическое поле внутри куба имеет пространственную зависимость $E(x,y,z)=E_0\sin(k_{x}x)\sin(k_{y}y)\sin(k_{z}z)$, при этом считается, что одна из вершин куба находится в начале координат, а стороны куба направлены вдоль осей $x,y$ и $z$ соответственно. Пусть $h$ — постоянная Планка, $k_{B}$ — постоянная Больцмана, $c$ — скорость света.
а) Электрическое поле должно быть равно нулю на всех гранях куба. Каковы возможные значения $k_{x},k_{y}$ и $k_{z}$?
б) В этой модели каждому возможному набору значений $(k_{x},k_{y}$,$k_{z})$ соответствует одно так называемое квантовое состояние. Все возможные квантовые состояния могут быть изображены точками в так называемом пространстве состояний, представляющем собой воображаемое пространство с введенными декартовыми координатами $k_{x},k_{y}$ и $k_{z}$. Сколько состояний $N$ находится в некотором объеме $s$ пространства состояний? $s$ настолько велико, что дискретностью квантовых состояний можно пренебречь;
в) Каждому квантовому состоянию может соответствовать фотон с частотой $\omega=c|k|$, где $|k|=\sqrt{k_{x}^2+k_{y}^2+k_{z}^2}$. Пусть температура системы равна $T$. Известно, что ни один фотон не может иметь энергию, большую чем $k_{B}T$. Определите форму и размеры области в пространстве состояний, которая может быть занята фотонами;
г) Пусть каждое возможное квантовое состояние занято одним фотоном. Найдите полную энергию всех фотонов в кубе. Считайте, что температура настолько высока, что внутри куба находится очень большое число квантовых состояний. Подсказка: надо разделить пространство состояний на сферические слои.
комментарий/решение