7-я олимпиада им. Шалтая Смагулова, 7 класс, 1 тур

Есеп №1. $7^{4n - 1}\times49^{3n} = 7^{9}$ теңдеуінен $n$ санын анықтаңыз.
комментарий/решение

Есеп №2. $ABC$ үшбұрышында $BC$ қабырғасында $D$ нүктесі $AD = DC = AB$ және $\angle BAD=28^\circ$ болатындай белгіленген. $BAC$ бұрышы неше градусқа тең?
комментарий/решение

Есеп №3. $8\times8$ өлшемді шахмат тақтасынан, ортақ қабырғасы бар екі торкөзді неше түрлі әдіспен таңдауға болады?
комментарий/решение

Есеп №4. $\frac{1}{10!} + \frac{1}{11!} = \frac{x}{12!}$ теңдеуінен $x$ санын анықтаңыз. (Әдеттегідей, $n!$ деген 1-ден $n$-ге дейінгі барлық натурал сандардың көбейтіндісін білдіреді, яғни $n!=1\cdot 2\cdot \ldots \cdot n$.)
комментарий/решение

Есеп №5. Асан 200-ден үлкен бірақ 220-дан кіші натурал санды жасырды. Егер ол жасырған санды 3-ке көбейтіп, көбейтіндіге 36-ны қосып, қосындыны 3-ке бөліп, бөліндіден 12-ні азайтса, нәтижесінде жай сан шығады. Асан қандай сан жасырған?
комментарий/решение

Есеп №6. Бір мектепке олимпиадаға келген 6 және 7-сынып оқушыларының жалпы саны 50-ден аспаған. Мұғалім, әр партада бір 6-сынып және бір 7-сынып оқушысы отыратындай етіп, бірінші аудиторияны толығымен толтырған. Сонда бірінші аудиторияға 6-сыныптардың 3/4-і, ал 7-сыныптардың 4/5-і кірген. Бірінші аудиторияға қанша оқушы кірген?
комментарий/решение

Есеп №7. Әртүрлі ${x}$ және ${y}$ сандары $11{x}^{2} - 2024{x} = 11{y}^{2} - 2024{y}$ теңдігін қанағаттандырады. ${x} + {y}$ қосындысын тап.
комментарий/решение

Есеп №8. Асанға үш түрлі деңгейдегі 50 есеп берген, олар — жеңіл, орташа және күрделі есептер. Жеңіл есеп саны орташа есеп санынан 11 есе көп. Күрделі есеп саны жеңіл есеп санынан аз, бірақ орташа есеп санынан көп. Асанға неше күрделі есеп берген?
комментарий/решение

Есеп №9. $||2x-4|-6|=2024$ теңдеуінің барлық түбірлерінің қосындысын тап.
комментарий/решение

Есеп №10. $p, q$ жай сандары $17p + 3q = 2017$ теңдігін қанағаттандыратыны белгілі болса, $p+q$ қосындысы нешеге тең?
комментарий/решение

Есеп №11. Тоғыз ұяшыққа 1, 2, $\ldots$, 9 сандары дәл бір бірден жазылып, әр жолда және әр бағанда көрсетілген амалдар орындалды. Алмалардың нәтижелері дөңгелектерге жазылды (суретті қараңыз). Жұлдызшамен белгіленген ұяшықта қандай сан жазылған?

комментарий/решение

Есеп №12. Үй қаймағының майлылығы 45$\%$, ал дүкеннен алынған қаймақтікі 12$\%$-ға тең. Әже үй қаймағын дүкен қаймағымен араластырып, майлылығы 32$\%$ болатын 1650 грамм қаймақ алды. Араластырғанға дейін дүкен қаймағының салмағы неше грамм болған?
комментарий/решение

Есеп №13. Суретте төрт шаршының көмегі арқылы пайда болған төрт бөліктің үшеуінің ауданы көрсетілген (оның ішінде екі аудан ол шеткі екі шаршының ауданы). Сұрланған шаршының ауданы нешеге тең?

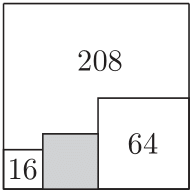
комментарий/решение

Есеп №14. Суретте кіші дұрыс үшбұрыштың екі төбесі үлкен дұрыс үшбұрыштың қабырғасында жатыр. Сонда суреттегі пайда болған бұрыштың бірі екіншісінен 4 есе үлкен. $\alpha$ бұрышы неше градусқа тең?

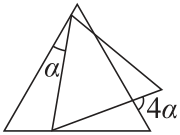
комментарий/решение

Есеп №15. Қабырғалары натурал сан болатын және периметрі 20-ға тең неше түрлі үшбұрыштар бар?
комментарий/решение

Есеп №16. $5880 \cdot n$ көбейтіндісі натурал санның кубы болатындай, ең кіші натурал $n$ санын табыңыз.
комментарий/решение

Есеп №17. 2449 санымен өзара жай және осы саннан кіші неше натурал сан бар? (Егер екі бүтін сандардың ең үлкен ортақ бөлгіші $1$-ге тең болса, ондай сандарды өзара жай сан деп атаймыз.)
комментарий/решение(1)

Есеп №18. $999 \ldots 9^2$ санының (9 цифры 23 рет қайталанады) цифрларының қосындысын табыңыз.
комментарий/решение

Есеп №19. Үшбұрышта «чевиана» деп үшбұрыштың төбесі мен қарама-қарсы қабырғада жатқан нүктені қосатын кесінді айтамыз. Периметрі 19 см-ге тең үшбұрыш өзінің үш чевианасымен 4 үшбұрыш пен 3 төртбұрышқа бөлінген (суретті қараңыз). Осы үш төртбұрыштың периметрлерінің қосындысы 25 см, ал төрт үшбұрыштың периметрлерінің қосындысы 20 см болса, үш чевиананың ұзындықтарының қосындысы неше сантиметрге тең?

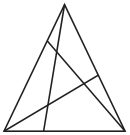
комментарий/решение

Есеп №20. Қабырғада тілшелі сағат ілініп тұр (суретті қараңыз). Бұзақы Петя минуттық пен сағаттық тілдерді қалдырып, секундтық тілді жұлып алды. Минуттық және сағаттық тілшелер көлденең сызықпен, сәйкесінше, $\alpha$ және $2\alpha$ бұрыштарын құраған кезде секундтық тіл неше секундтты көрсетер еді? (Жауап 0 мен 59 аралығындағы бүтін сан түрінде берілуі керек.)

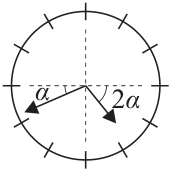
комментарий/решение