7-я олимпиада им. Шалтая Смагулова, 7 класс, 1 тур

Задача №1. Из уравнения $7^{4n - 1}\times49^{3n} = 7^{9}$ найдите число $n$.
комментарий/решение

Задача №2. В треугольнике $ABC$ на стороне $BC$ отмечена точка $D$ такая, что $AD = DC = AB$ и $\angle BAD=28^\circ$. Скольким градусам равен угол $BAC$?
комментарий/решение

Задача №3. Сколькими способами с клетчатой доски $8 \times 8$ можно выбрать две клетки, имеющие общую сторону?
комментарий/решение

Задача №4. Из уравнения $\frac{1}{10!} + \frac{1}{11!} = \frac{x}{12!}$ найдите число $x$. (Как обычно, $n!$ означает произведение всех натуральных чисел от 1 до $n$, то есть $n!=1\cdot 2\cdot \ldots \cdot n$.)
комментарий/решение

Задача №5. Асан загадал целое число больше 200, но меньше 220. Если он умножит загаданное число на 3, прибавит к произведению 36, разделит сумму на 3 и вычтет 12 из частного, то полученный результат будет простым числом. Какое число загадал Асан?
комментарий/решение

Задача №6. Из одной школы на олимпиаду пришли учащихся 6 и 7 классов. Общее количество участников не превышало 50. Учитель сначала полностью заполнил 1-ю аудиторию, посадив за каждую парту по одному шестикласснику и одному семикласснику, остальных отправил в другую аудиторию. Оказалось, что в 1-ю аудиторию вошли 3/4 всех шестиклассников и 4/5 всех семиклассников. Сколько учеников вошли в первую аудиторию?
комментарий/решение

Задача №7. Для различных чисел ${x}$ и ${y}$ выполнено равенство: $11{x}^{2} - 2024{x} = 11{y}^{2} - 2024{y}$. Найдите сумму ${x} + {y}$.
комментарий/решение

Задача №8. Асану дали 50 задач трёх сложностей — легкие, средние и сложные. Легких задач в 11 раз больше, чем средних. Число сложных задач меньше легких, но больше средних. Сколько сложных задач дали Асану?
комментарий/решение

Задача №9. Найдите сумму всех корней уравнения: $||2x-4|-6|=2024$.
комментарий/решение

Задача №10. Для простых чисел $p$ и $q$ выполнено равенство $17p + 3q = 2017$. Найдите сумму $p+q$.
комментарий/решение

Задача №11. Числа 1, 2, $\ldots$, 9 вписали в 9 клеток по одному разу, и выполнили действия, указанные в каждой строчке и каждом столбце. Результаты действий записали в кружках (см. рис.). Какое число написано в клетке, отмеченной звездочкой?

комментарий/решение

Задача №12. Жирность домашней сметаны равна 45$\%$, а магазинного — 12$\%$. Бабушка смешала несколько граммов домашней сметаны с несколькими граммами магазинной и получила 1650 граммов сметаны 32$\%$ жирности. Сколько граммов магазинной сметаны было до смешивания?
комментарий/решение

Задача №13. На рисунке четыре квадрата образуют четыре части. Площади трех из них указаны в соответствующих частях (из них две площади — это площади двух крайних квадратов). Найдите площадь квадрата, закрашенного серым цветом.

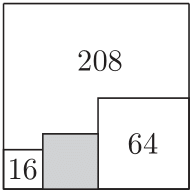
комментарий/решение

Задача №14. На рисунке две вершины меньшего правильного треугольника лежат на двух сторонах большего правильного треугольника, причем полученные углы на рисунке отличаются в 4 раза. Скольким градусам равен угол $\alpha$?

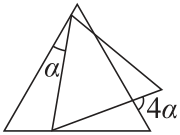
комментарий/решение

Задача №15. Сколько существует различных треугольников с натуральными сторонами и с периметром 20?
комментарий/решение

Задача №16. Найдите наименьшее натуральное число $n$ такое, что произведение $5880 \cdot n$ равно кубу натурального числа.
комментарий/решение

Задача №17. Найдите количество натуральных чисел, меньших чем 2449, и взаимно простых с ним. (Два целых числа называются взаимно простыми, если их наибольший общий делитель равен единице.)
комментарий/решение(1)

Задача №18. Найдите сумму цифр числа $999 \ldots 9^2$ (девятка встречается 23 раза).
комментарий/решение

Задача №19. «Чевианой» треугольника назовем отрезок, соединяющий вершину с точкой, лежащей на противоположной стороне. Треугольник, периметр которого равен 19 см, разбит тремя чевианами на 4 треугольника и 3 четырехугольника (см. рис.). Сумма периметров трех четырехугольников равна 25 см, а сумма периметров четырех треугольников равна 20 см. Скольким сантиметрам равна сумма длин трёх чевиан этого треугольника.

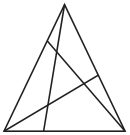
комментарий/решение

Задача №20. На стене висят стрелочные часы. Хулиган Петя вырвал секундную стрелку, оставив только минутную и часовую. Какое время (в секундах) показывала бы секундная стрелка в момент, когда минутная и часовая стрелки соответственно образовывали углы $\alpha$ и $2\alpha$ с горизонтальной линией (см. рис.). (Ответ дайте в виде целого числа от 0 до 59.)

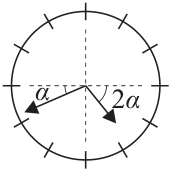
комментарий/решение