10-я международная Иранская олимпиада по геометрии, 2023 год, первая лига, 7-8 классы

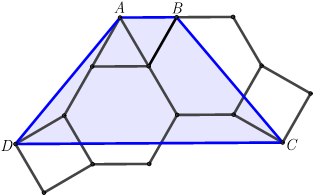
Есеп №1. Төменгі суреттегі барлық көпбұрыштар — дұрыс көпбұрыштар.

$ABCD$ — теңбүйірлі трапеция екенін дәлелдеңіз.

комментарий/решение(8)

Есеп №2.

$ABC$ үшбұрышында

$AB=AC$ және

$\angle A=30^\circ$ , ал

$L$ және

$M$ нүктелері, сәйкесінше,

$AB$ және

$AC$ қабырғаларынан

$AL=CM$ болатындай алынған.

$AB$ кесіндісінде

$K$ нүктесі

$\angle AMK= 45^\circ$ болатындай алынған. Егер

$\angle LMC=75^\circ$ болса,

$KM+ML=BC$ екенін дәлелдеңіз.
комментарий/решение(2)

Есеп №3.

$ABCD$ — қабырғасы 1-ге тең квадрат. Квадраттың ішінде (қабырғаларында емес) жататын неше

$P$ нүкте үшін осы квадратты аудандары өзара тең 10 үшбұрыштарға, әрі әр үшбұрыштың ортақ төбесі

$P$ нүктесі болатындай, үшбұрыштарға бөлуге болады?
комментарий/решение(1)

Есеп №4. Дөңес

$ABCD$ төртбұрышының диагоналдары

$E$ нүктесінде қиылысады. Егер

$CD = BC = BE$ болса,

$AD + DC \geq AB$ екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №5. Көпбұрыш өзара қиылыспайтын ішкі диагональдармен үшбұрыштарға бөлінген. Ортақ қабырғасы бар кез келген екі үшбұрыштың сол қабырғаға қарсы жатқан екі бұрыштардың қосындысы

$180^\circ$ -тан үлкен екені белгілі.
a) Осы көпбұрыштың дөңес екенін дәлелдеңіз.
b) Бастапқы көпбұрыш бөлінуде пайда болған әрбір үшбұрышқа сырттай сызылған шеңбердің ішінде жататынын дәлелдеңіз.
комментарий/решение