10-я международная Иранская олимпиада по геометрии, 2023 год, первая лига, 7-8 классы

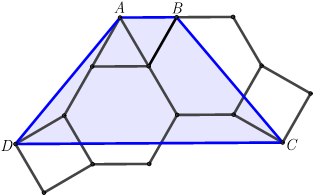
Задача №1. Все многоугольники на рисунке ниже являются правильными. Докажите, что

$ABCD$ — равнобедренная трапеция.

комментарий/решение(8)

Задача №2. В равнобедренном треугольнике

$ABC$ с

$AB=AC$ и

$\angle A=30^\circ$ , точки

$L$ и

$M$ лежат на сторонах

$AB$ и

$AC$ соответственно так, что

$AL=CM$ . Точка

$K$ отмечена на отрезке

$AB$ так, что

$\angle AMK= 45^\circ$ . Докажите, что если

$\angle LMC=75^\circ$ , то

$KM+ML=BC$ .
комментарий/решение(2)

Задача №3. Пусть

$ABCD$ — квадрат со стороной

$1$ . Сколько точек

$P$ внутри квадрата (не на его сторонах) имеют свойство, что квадрат можно разрезать на 10 треугольников равных площадей, и все они имеют общую вершину в точке

$P$ ?
комментарий/решение(1)

Задача №4. Диагонали выпуклого четырёхугольника

$ABCD$ пересекаются в точке

$E$ . Предположим, что

$CD = BC = BE$ . Докажите, что

$AD + DC \geq AB$ .
комментарий/решение(1)

Задача №5. Многоугольник разбит на треугольники с помощью проведения непересекающихся внутренних диагоналей таким образом, что для каждой пары треугольников, имеющих общую сторону, сумма углов, противоположных этой общей стороне, больше

$180^\circ$ .
a) Докажите, что этот многоугольник является выпуклым.
b) Докажите, что описанная окружность каждого треугольника, используемого в разбиении, содержит весь многоугольник.
комментарий/решение