Леонард Эйлер атындағы олимпиада,2014-2015 оқу жылы, қорытынды кезеңнің 2-ші туры

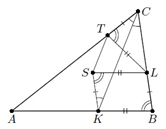
$CK$ — $ABC$ үшбұрышының биссектрисасы. $BC$ және $AC$ қабырғаларынан $CT=BL$ және $TL=BK$ болатындай сәйкесінше $L$ және $T$ нүктелері алынған. $LTC$ үшбұрышы алдыңғы үшбұрышқа ұқсас екенін дәлелдеңіз. ( С. Берлов )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Отметим такую точку $S$, что $BLSK$ — параллелограмм. Если $S$ совпала с $T$, то подобие очевидно. Если же $S$ не совпала с $T$, то поскольку $CT = BL = KS$ и $\angle SKC = \angle KCL = \angle KCA$, точки $K$, $C$, $T$, $S$ — вершины равнобедренной трапеции. Так как $TL = KB = LS$, то точка $L$ лежит на оси симметрии этой трапеции, следовательно, $\angle CTL = \angle KSL = \angle KBL$, откуда и следует требуемое подобие.