Олимпиада имени Леонарда Эйлера2012-2013 учебный год, II тур регионального этапа

В клетках доски $8 \times 8$ расставлены числа $1$ и $-1$ (в каждой клетке — по одному числу). Рассмотрим всевозможные расположения четырёхклеточной фигурки на доске (фигурку можно поворачивать, но её клетки не должны выходить за пределы доски). Назовём такое расположение неудачным, если сумма чисел, стоящих в четырёх клетках фигурки, не равна 0. Найдите наименьшее возможное число неудачных расположений. ( М. Антипов )

Комментарий/решение

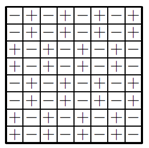
Комментарии от администратора Комментарии от администратора №1.     Ответ. 36.
Решение. Покажем, что в каждом «кресте» из пяти клеток доски найдётся хотя бы одно неудачное расположение. Предположим противное; пусть в крайних клетках креста стоят числа $a$, $b$, $c$, $d$, а в центральной — $e$; обозначим через $S$ сумму всех этих пяти чисел. Тогда по нашему предположению $S-a = S-b = S-c = S-d = 0$, откуда $a = b = c = d$. Но в таком случае $e = -(a+b+c) = -3a$, что невозможно. Поскольку каждое расположение фигурки лежит не более, чем в одном кресте, получается, что в 36 крестах (с центрами во всех не крайних клетках) найдётся не менее 36 неудачных расположений. С другой стороны, на рисунке показан пример расстановки, при которой количество неудачных расположений равно 36 (в каждой клетке указан знак соответствующего числа). Действительно, в любом кресте неудачное расположение ровно одно, а все расположения, прилегающие длинной стороной к границе доски — удачные.