Эйлер атындағы олимпиада, 2012-2013 оқу жылы, аймақтық кезеңнің 2 туры

$8\times 8$ тақтасының шаршыларына 1 мен ${-1}$ сандары қойылған (әр шаршыда бір ғана саннан). Тақтадағы төрт шаршылы фигурасының барлық мүмкін орналасуын қарастырайық (фигурканы бұруға болады, бірақ оның шаршылары тақтадан тыс шықпау керек). Орналасқан фигураның төрт шаршысындағы сандар қосындысы нөлге тең болмаса, ондай орналасуды сәтсіз деп атайық. Мүмкін болатын ең аз сәтсіз орналасу санын табыңыз. ( М. Антипов )

Комментарий/решение

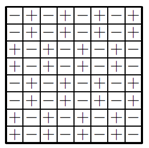
Комментарии от администратора Комментарии от администратора №1.     Ответ. 36.
Решение. Покажем, что в каждом «кресте» из пяти клеток доски найдётся хотя бы одно неудачное расположение. Предположим противное; пусть в крайних клетках креста стоят числа $a$, $b$, $c$, $d$, а в центральной — $e$; обозначим через $S$ сумму всех этих пяти чисел. Тогда по нашему предположению $S-a = S-b = S-c = S-d = 0$, откуда $a = b = c = d$. Но в таком случае $e = -(a+b+c) = -3a$, что невозможно. Поскольку каждое расположение фигурки лежит не более, чем в одном кресте, получается, что в 36 крестах (с центрами во всех не крайних клетках) найдётся не менее 36 неудачных расположений. С другой стороны, на рисунке показан пример расстановки, при которой количество неудачных расположений равно 36 (в каждой клетке указан знак соответствующего числа). Действительно, в любом кресте неудачное расположение ровно одно, а все расположения, прилегающие длинной стороной к границе доски — удачные.