Областная олимпиада по физике, 2020 год, 9 класс, теоретический тур

Задача №1. (9 баллов). Космические скорости используются как характерные критические скорости движения космических объектов в гравитационных полях небесных тел и их систем. Третья космическая скорость является минимальной скоростью, которую необходимо сообщить ракете относительно Земли, чтобы она навсегда покинула пределы Солнечной системы и ушла в бесконечность. Предположим, что ракета под углом в

$\theta$ направлению орбитального движения Земли вокруг Солнца выходит из зоны действия земного тяготения. Найдите приближенное значение третей космической скорости. Считать, что кроме Земли и Солнца на ракету никакие другие тела не действуют. Численные значения массы и радиуса Земли соответственно равны

$M_\text{З}=5,97 \cdot 10^{24}$ кг,

$r_\text{З}=6400$ км, круговая скорость движения ракеты относительно Солнца

$V_\text{К}=29,8$ км/с, гравитационная постоянная

$G=6,67 \cdot 10^{-11}$ м

$^3$ /(кг

$\cdot$ с

$^2$ ).
комментарий/решение

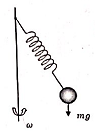
Задача №2. (7 баллов). На пружину жесткости

$k$ и начальной длины

$l_0$ подвешен шарик массы

$m$ . Система находиться над центром платформы центробежной машины (см. рисунок). Когда машину приводят в движение, шарик начинает вращаться вместе с ней с угловой скоростью

$\omega$ . Считая пружину идеальной, определите угол

$\alpha$ , который образуется между пружиной и вертикалью.

комментарий/решение(1)

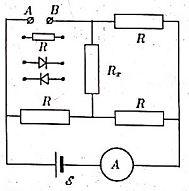
Задача №3. (7 баллов). К точкам

$A$ и

$B$ цепи, представленной на рисунке, можно подключать резистор или диод. Сопротивление резистора равно

$R$ ив точности совпадает с сопротивлением диода при прямом соединении, а в обратном соединении сопротивление диода много больше заданного

$R$ . Найдите для каждого из трех возможных способов подключений зависимость показаний амперметра от сопротивления

$R_x$ . Постройте графики полученных зависимостей.

комментарий/решение

Задача №4. (7 баллов). Треугольник располагают перед линзой так, что один из его катетов лежит на главной оптической оси линзы (см. рисунок). Расстояние между ближайшей точкой треугольника к линзе и центром самой линзы равно

$2F$ . Треугольник считать равнобедренным и прямоугольным, а его площадь равной 50 см

$^2$ . Линзу считать тонкой собирающей, а ее фокусное расстояние равным 50 см. Постройте изображение данного треугольника и найдите площадь получившейся фигуры.

комментарий/решение