Областная олимпиада по физике, 9 класс, теоретический тур

7 ұпай). Қатаңдығы $k$ және бастапқы ұзындығы $l_0$ болатын серіппеге массасы $m$ шарик ілінген. Жүйе, центрдентепкіш машина платформасының центрінің үстінде, орналасқан (суретті қараңыз). Машинаны іске қосып, қозғалтқан кезде, шарик онымен бірге $\omega$ бұрыштық жылдамдықпен айнала бастайды. Серіппені идеал деп есептеп, серіппе мен вертикаль арасындағы $\alpha$ бұрышты анықтаңыз.

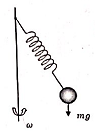
Комментарий/решение

По формуле центробежной массе шарика $Fg=mw^2•R$

Где R растояние шарика от палки. $Fo=k•x_0$

$R=(l_0+x_0)•sin a$

$Fg=mw^2(l_0+x_0)sin a$

И так как нам известен mg тогда и теперь записываем уравнение по координатам х и у.