12-я Жаутыковская олимпиада (2016), теоретический тур
Задача №1. (10,0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача 1А (4.0 балла) Однородная планета радиуса $R$ не имеет атмосферы и не вращается. С поверхности планеты бросают камень под углом $\alpha$ к горизонту со скоростью $\vartheta_0$, равной первой космической скорости на поверхности этой планеты. Найдите максимальную высоту подъёма камня над поверхностью планеты. На каком расстоянии от места броска, измеренном вдоль поверхности, камень упадёт?
Задача 1В (3.0 балла)
Задача 1С (3.0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача 1А (4.0 балла) Однородная планета радиуса $R$ не имеет атмосферы и не вращается. С поверхности планеты бросают камень под углом $\alpha$ к горизонту со скоростью $\vartheta_0$, равной первой космической скорости на поверхности этой планеты. Найдите максимальную высоту подъёма камня над поверхностью планеты. На каком расстоянии от места броска, измеренном вдоль поверхности, камень упадёт?
Задача 1В (3.0 балла)
Задача 1С (3.0 балла)
Задача №2. Равновесие с энергетической точки зрения (10,0 балла)
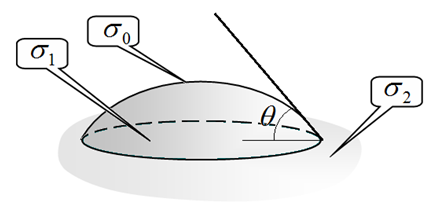
$\sigma_0$ — поверхностное натяжение на границе жидкости с газом;
$\sigma_1$ — поверхностное натяжение на границе жидкости с твердым телом;
$\sigma_2$ — поверхностное натяжение на границе твердого тела с газом;
$\theta$ — краевой угол (угол смачивания). Величины $\sigma_0$, $\sigma_1$, $\sigma_2$ имеют смысл поверхностной энергии, приходящейся на единицу площади контакта сред. Во всех частях задачи используйте следующие численные значения для воды: поверхностное натяжение $\sigma_0=0,072$ Н/м; краевой угол $\theta=20^{\circ}$; плотность жидкости $\rho=10^3$ кг/м$^3$; ускорение свободного падения $g=9,8$ м/с$^2$.
1. Введение (1,0 балла)
1. [1,0 балла] Докажите, что изменение поверхностной энергии на границе жидкости и твердого тела определяется формулой $$\Delta U_{S}=-\sigma_0 \cos\theta \Delta S,\quad (1)$$ где $\Delta S$ — изменение площади соприкосновения жидкости с твердым телом.
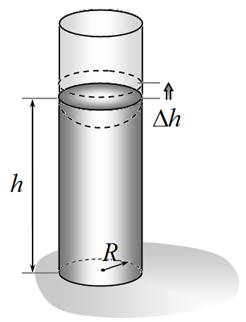
2. Вода в вертикальной цилиндрической трубке (2,0 балла)
Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
2.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $U_{G}$ при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.3 [1,0 балла] Используя принцип минимума потенциальной энергии, найдите высоту подъема воды в трубке $h_0$ в состоянии равновесия. Рассчитайте численное значение этой величины.
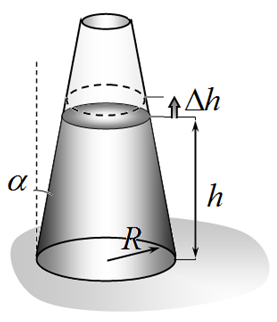
3. Вода в вертикальной конической трубке (4,0 балла)
Внимание: В дальнейшем изменение поверхностной энергии на границе жидкости и воздуха не учитывайте. Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
3.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
3.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $\Delta U{G}$ при дополнительном поднятии воды в трубке на малую высоту $h$.
3.3 [1,0 балла] Получите уравнение для определения высоты подъема воды в трубке $h_1$ в состоянии равновесия и выразите параметры этого уравнения через $\sigma_0$, $\theta$, $\alpha$ и найденную в п.2.3 высоту $h_0$.
3.4 [1,0 балла] Пусть угол $\alpha=10^{-2}$ рад. Трубку частично заполняют водой до некоторого уровня $H$. Найдите зависимость установившейся высоты уровня воды в трубке от $H$.
3.5 [1,0 балла] Укажите диапазон углов $\alpha$ (и его численные значения) при котором вода полностью заполнит трубку.
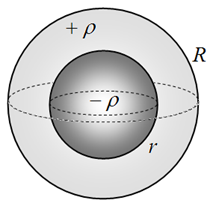
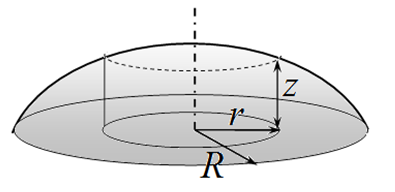
4. Вытекание воды (3,0 балла)
4.1 [3,0 балла] При каком минимальном значении радиусов отверстий вода начнет вытекать из бутылки?
Математические подсказки.
Небольшую выпуклость сферической формы можно приближенно описать функцией $$z=h\left(\ 1-\frac{r^2}{R^2} \right),$$ где $R$ — радиус выпуклости, $h$ — ее высота, причем $h\ll R$. Тогда с точностью до малых величин высшего порядка: площадь ее сферической части равна $$S=\pi(R^2+h^2),$$ а потенциальная энергия в поле тяжести $$U=\frac{\pi R^2 h^2}{6}\rho g.$$
комментарий/решение
$\sigma_0$ — поверхностное натяжение на границе жидкости с газом;
$\sigma_1$ — поверхностное натяжение на границе жидкости с твердым телом;
$\sigma_2$ — поверхностное натяжение на границе твердого тела с газом;
$\theta$ — краевой угол (угол смачивания). Величины $\sigma_0$, $\sigma_1$, $\sigma_2$ имеют смысл поверхностной энергии, приходящейся на единицу площади контакта сред. Во всех частях задачи используйте следующие численные значения для воды: поверхностное натяжение $\sigma_0=0,072$ Н/м; краевой угол $\theta=20^{\circ}$; плотность жидкости $\rho=10^3$ кг/м$^3$; ускорение свободного падения $g=9,8$ м/с$^2$.
1. Введение (1,0 балла)
1. [1,0 балла] Докажите, что изменение поверхностной энергии на границе жидкости и твердого тела определяется формулой $$\Delta U_{S}=-\sigma_0 \cos\theta \Delta S,\quad (1)$$ где $\Delta S$ — изменение площади соприкосновения жидкости с твердым телом.
2. Вода в вертикальной цилиндрической трубке (2,0 балла)
Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
2.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $U_{G}$ при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.3 [1,0 балла] Используя принцип минимума потенциальной энергии, найдите высоту подъема воды в трубке $h_0$ в состоянии равновесия. Рассчитайте численное значение этой величины.
3. Вода в вертикальной конической трубке (4,0 балла)
Внимание: В дальнейшем изменение поверхностной энергии на границе жидкости и воздуха не учитывайте. Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
3.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
3.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $\Delta U{G}$ при дополнительном поднятии воды в трубке на малую высоту $h$.
3.3 [1,0 балла] Получите уравнение для определения высоты подъема воды в трубке $h_1$ в состоянии равновесия и выразите параметры этого уравнения через $\sigma_0$, $\theta$, $\alpha$ и найденную в п.2.3 высоту $h_0$.
3.4 [1,0 балла] Пусть угол $\alpha=10^{-2}$ рад. Трубку частично заполняют водой до некоторого уровня $H$. Найдите зависимость установившейся высоты уровня воды в трубке от $H$.
3.5 [1,0 балла] Укажите диапазон углов $\alpha$ (и его численные значения) при котором вода полностью заполнит трубку.
4. Вытекание воды (3,0 балла)
4.1 [3,0 балла] При каком минимальном значении радиусов отверстий вода начнет вытекать из бутылки?
Математические подсказки.
Небольшую выпуклость сферической формы можно приближенно описать функцией $$z=h\left(\ 1-\frac{r^2}{R^2} \right),$$ где $R$ — радиус выпуклости, $h$ — ее высота, причем $h\ll R$. Тогда с точностью до малых величин высшего порядка: площадь ее сферической части равна $$S=\pi(R^2+h^2),$$ а потенциальная энергия в поле тяжести $$U=\frac{\pi R^2 h^2}{6}\rho g.$$
комментарий/решение
Задача №3. Нелинейный конденсатор (10,0 балла)
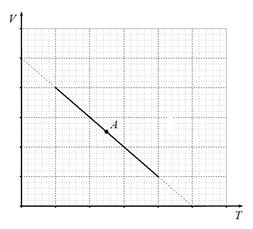
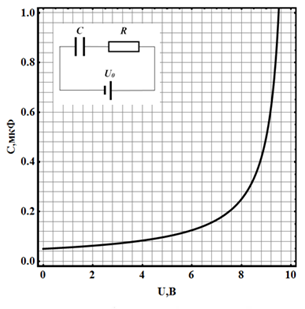
В электрическую схему с источником напряжения $U_0$ включены последовательно сопротивление $R=1$ кОм и нелинейный конденсатор, емкости которого зависит от напряжения, а соответствующий график показан на рисунке ниже.
Примечания: для выполненния задания вам может понадобиться клетчатая бумага, расположенная под графиком.
1. [0,75 балла] Пусть $U_0=5$ В. Определите заряд конденсатора, который установится на нем через достаточно большое время;
Пусть в начальный момент времени заряд на конденсаторе равен нулю, а источник дает напряжение $U_0=10$ В. Из графика видно, что емкость конденсатора при этом напряжении обращается в бесконечность, то есть $C(10 В)=\infty$.
2. [0,25 балла] Чему равно время зарядки конденсатора до напряжения $U_0=10$ В?
3. [3,0 балла] Определите момент времени $t$, когда заряд на конденсаторе станет равным $q=4$ мкКл;
4. [0,5 балла] В течении какого промежутка времени $\Delta t$ заряд на конденсаторе увеличится с $q_0=4$ мкКл до $q=8$ мкКл;
5. [0,5 балла] Найдите заряд конденсатора в момент времени $t_0=3$ мс; Пусть источник дает постоянное напряжение с небольшой добавкой переменного напряжения, так что $U_0=U+\delta U \sin\omega t =[5+0,1 \sin\omega t]$ В, где $\omega=2500$ рад/с. Через достаточно большое время в цепи установятся колебания напряжения и тока.
6. [0,5 балла] Чему равна разность фаз $\varphi$ между колебаниями напряжения на конденсаторе и сопротивлении?
7. [4,0 балла] Найдите зависимость силы тока в цепи $I(t)$ от времени;
8. [0,5 балла] Найдите зависимость напряжения $U_{C} (t)$ на конденсаторе от времени.
комментарий/решение
В электрическую схему с источником напряжения $U_0$ включены последовательно сопротивление $R=1$ кОм и нелинейный конденсатор, емкости которого зависит от напряжения, а соответствующий график показан на рисунке ниже.
Примечания: для выполненния задания вам может понадобиться клетчатая бумага, расположенная под графиком.
1. [0,75 балла] Пусть $U_0=5$ В. Определите заряд конденсатора, который установится на нем через достаточно большое время;
Пусть в начальный момент времени заряд на конденсаторе равен нулю, а источник дает напряжение $U_0=10$ В. Из графика видно, что емкость конденсатора при этом напряжении обращается в бесконечность, то есть $C(10 В)=\infty$.
2. [0,25 балла] Чему равно время зарядки конденсатора до напряжения $U_0=10$ В?
3. [3,0 балла] Определите момент времени $t$, когда заряд на конденсаторе станет равным $q=4$ мкКл;
4. [0,5 балла] В течении какого промежутка времени $\Delta t$ заряд на конденсаторе увеличится с $q_0=4$ мкКл до $q=8$ мкКл;
5. [0,5 балла] Найдите заряд конденсатора в момент времени $t_0=3$ мс; Пусть источник дает постоянное напряжение с небольшой добавкой переменного напряжения, так что $U_0=U+\delta U \sin\omega t =[5+0,1 \sin\omega t]$ В, где $\omega=2500$ рад/с. Через достаточно большое время в цепи установятся колебания напряжения и тока.
6. [0,5 балла] Чему равна разность фаз $\varphi$ между колебаниями напряжения на конденсаторе и сопротивлении?
7. [4,0 балла] Найдите зависимость силы тока в цепи $I(t)$ от времени;
8. [0,5 балла] Найдите зависимость напряжения $U_{C} (t)$ на конденсаторе от времени.
комментарий/решение