12-я Жаутыковская олимпиада (2016), теоретический тур
Равновесие с энергетической точки зрения (10,0 балла)
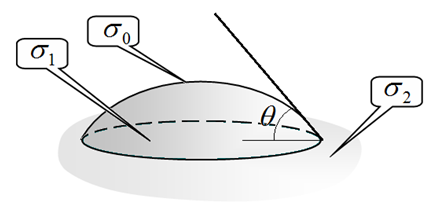
$\sigma_0$ — поверхностное натяжение на границе жидкости с газом;
$\sigma_1$ — поверхностное натяжение на границе жидкости с твердым телом;
$\sigma_2$ — поверхностное натяжение на границе твердого тела с газом;
$\theta$ — краевой угол (угол смачивания). Величины $\sigma_0$, $\sigma_1$, $\sigma_2$ имеют смысл поверхностной энергии, приходящейся на единицу площади контакта сред. Во всех частях задачи используйте следующие численные значения для воды: поверхностное натяжение $\sigma_0=0,072$ Н/м; краевой угол $\theta=20^{\circ}$; плотность жидкости $\rho=10^3$ кг/м$^3$; ускорение свободного падения $g=9,8$ м/с$^2$.
1. Введение (1,0 балла)
1. [1,0 балла] Докажите, что изменение поверхностной энергии на границе жидкости и твердого тела определяется формулой $$\Delta U_{S}=-\sigma_0 \cos\theta \Delta S,\quad (1)$$ где $\Delta S$ — изменение площади соприкосновения жидкости с твердым телом.
2. Вода в вертикальной цилиндрической трубке (2,0 балла)
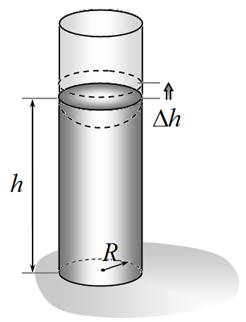
Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
2.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $U_{G}$ при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.3 [1,0 балла] Используя принцип минимума потенциальной энергии, найдите высоту подъема воды в трубке $h_0$ в состоянии равновесия. Рассчитайте численное значение этой величины.
3. Вода в вертикальной конической трубке (4,0 балла)
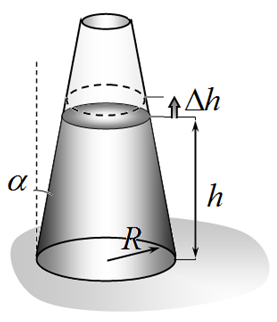
Внимание: В дальнейшем изменение поверхностной энергии на границе жидкости и воздуха не учитывайте. Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
3.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
3.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $\Delta U{G}$ при дополнительном поднятии воды в трубке на малую высоту $h$.
3.3 [1,0 балла] Получите уравнение для определения высоты подъема воды в трубке $h_1$ в состоянии равновесия и выразите параметры этого уравнения через $\sigma_0$, $\theta$, $\alpha$ и найденную в п.2.3 высоту $h_0$.
3.4 [1,0 балла] Пусть угол $\alpha=10^{-2}$ рад. Трубку частично заполняют водой до некоторого уровня $H$. Найдите зависимость установившейся высоты уровня воды в трубке от $H$.
3.5 [1,0 балла] Укажите диапазон углов $\alpha$ (и его численные значения) при котором вода полностью заполнит трубку.
4. Вытекание воды (3,0 балла)
4.1 [3,0 балла] При каком минимальном значении радиусов отверстий вода начнет вытекать из бутылки?
Математические подсказки.
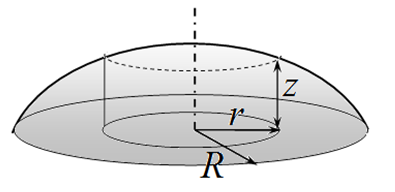
Небольшую выпуклость сферической формы можно приближенно описать функцией $$z=h\left(\ 1-\frac{r^2}{R^2} \right),$$ где $R$ — радиус выпуклости, $h$ — ее высота, причем $h\ll R$. Тогда с точностью до малых величин высшего порядка: площадь ее сферической части равна $$S=\pi(R^2+h^2),$$ а потенциальная энергия в поле тяжести $$U=\frac{\pi R^2 h^2}{6}\rho g.$$
посмотреть в олимпиаде
$\sigma_0$ — поверхностное натяжение на границе жидкости с газом;
$\sigma_1$ — поверхностное натяжение на границе жидкости с твердым телом;
$\sigma_2$ — поверхностное натяжение на границе твердого тела с газом;
$\theta$ — краевой угол (угол смачивания). Величины $\sigma_0$, $\sigma_1$, $\sigma_2$ имеют смысл поверхностной энергии, приходящейся на единицу площади контакта сред. Во всех частях задачи используйте следующие численные значения для воды: поверхностное натяжение $\sigma_0=0,072$ Н/м; краевой угол $\theta=20^{\circ}$; плотность жидкости $\rho=10^3$ кг/м$^3$; ускорение свободного падения $g=9,8$ м/с$^2$.
1. Введение (1,0 балла)
1. [1,0 балла] Докажите, что изменение поверхностной энергии на границе жидкости и твердого тела определяется формулой $$\Delta U_{S}=-\sigma_0 \cos\theta \Delta S,\quad (1)$$ где $\Delta S$ — изменение площади соприкосновения жидкости с твердым телом.
2. Вода в вертикальной цилиндрической трубке (2,0 балла)
Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
2.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $U_{G}$ при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
2.3 [1,0 балла] Используя принцип минимума потенциальной энергии, найдите высоту подъема воды в трубке $h_0$ в состоянии равновесия. Рассчитайте численное значение этой величины.
3. Вода в вертикальной конической трубке (4,0 балла)
Внимание: В дальнейшем изменение поверхностной энергии на границе жидкости и воздуха не учитывайте. Пусть уровень воды в трубке находится на некоторой высоте $h$, не обязательно соответствующей положению равновесия.
3.1 [0,5 балла] Запишите формулу для изменения поверхностной энергии $\Delta U_{S}$ системы при дополнительном поднятии воды в трубке на малую высоту $\Delta h$.
3.2 [0,5 балла] Запишите формулу для изменения потенциальной энергии жидкости в поле тяжести $\Delta U{G}$ при дополнительном поднятии воды в трубке на малую высоту $h$.
3.3 [1,0 балла] Получите уравнение для определения высоты подъема воды в трубке $h_1$ в состоянии равновесия и выразите параметры этого уравнения через $\sigma_0$, $\theta$, $\alpha$ и найденную в п.2.3 высоту $h_0$.
3.4 [1,0 балла] Пусть угол $\alpha=10^{-2}$ рад. Трубку частично заполняют водой до некоторого уровня $H$. Найдите зависимость установившейся высоты уровня воды в трубке от $H$.
3.5 [1,0 балла] Укажите диапазон углов $\alpha$ (и его численные значения) при котором вода полностью заполнит трубку.
4. Вытекание воды (3,0 балла)
4.1 [3,0 балла] При каком минимальном значении радиусов отверстий вода начнет вытекать из бутылки?
Математические подсказки.
Небольшую выпуклость сферической формы можно приближенно описать функцией $$z=h\left(\ 1-\frac{r^2}{R^2} \right),$$ где $R$ — радиус выпуклости, $h$ — ее высота, причем $h\ll R$. Тогда с точностью до малых величин высшего порядка: площадь ее сферической части равна $$S=\pi(R^2+h^2),$$ а потенциальная энергия в поле тяжести $$U=\frac{\pi R^2 h^2}{6}\rho g.$$
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.