Республиканская олимпиада по физике 2012, 10 класс, теоретический тур
Задача №1. Катастрофы (8 баллов)
Часть А. Цунами (3 балла)
Человек, находящийся на суше, замечает цунами, которое приближается к нему со скоростью $\vartheta= 25$ км/ч и имеет ширину $L= 100$ м. Человек находится прямо напротив середины фронта цунами на расстоянии $l=50$ м от него. Чтобы спастись, он начинает бежать с некоторой постоянной скоростью в неизменном направлении.
1. С какой минимальной скоростью $u_{\min}$ должен бежать человек, чтобы не попасть под цунами?
2. Под каким углом к фронту цунами должен двигаться человек, если он двигается со скоростью $u_{\min}$?
Часть В. Лавина (3 балла) Человек катается на лыжах по склону горы, которую можно считать наклонной плоскостью. В некоторый момент времени он замечает, что сверху срывается лавина шириной $L=100$ м, движущаяся с постоянным ускорением $a=5,0$ м/с$^2$. Человек находится прямо напротив середины фронта лавины на расстоянии $l=100$ м от нее. Чтобы спастись, он начинает ехать с некоторой постоянной скоростью в неизменном направлении.
1. С какой минимальной скоростью $u_{\min}$ должен ехать человек, чтобы не попасть под лавину?
2. Под каким углом к фронту лавины должен двигаться человек, если он двигается со скоростью $u_{\min}$?
Часть С. Черная дыра (2 балла) Космический корабль попадает в черную дыру и начинает падать на нее с начального расстояния $R$ по спирали таким образом, что его радиальная $\vartheta_{r}$ и тангенциальная $\vartheta_{t}$, скорости зависят от расстояния $r$ до центра черной дыры по закону: $\vartheta_{r}=\alpha/r$ и $\vartheta_{t}=\beta r^{2}$, где $\alpha$ и $\beta$ — некоторые известные постоянные величины. Радиальная скорость — это компонента вектора скорости $\vartheta$, направленная к центру черной дыры, а тангенциальная скорость — это компонента , перпендикулярная радиальной.
1. Какой угол составляет вектор скорости $\vartheta$ с направлением на центр черной дыры в момент времени, когда расстояние до центра черной дыры сократилось вдвое и стало равным $R/2$?
2. Сколько времени прошло от начала падения до этого момента времени?
комментарий/решение(1)
Часть А. Цунами (3 балла)
Человек, находящийся на суше, замечает цунами, которое приближается к нему со скоростью $\vartheta= 25$ км/ч и имеет ширину $L= 100$ м. Человек находится прямо напротив середины фронта цунами на расстоянии $l=50$ м от него. Чтобы спастись, он начинает бежать с некоторой постоянной скоростью в неизменном направлении.
1. С какой минимальной скоростью $u_{\min}$ должен бежать человек, чтобы не попасть под цунами?
2. Под каким углом к фронту цунами должен двигаться человек, если он двигается со скоростью $u_{\min}$?

Часть В. Лавина (3 балла) Человек катается на лыжах по склону горы, которую можно считать наклонной плоскостью. В некоторый момент времени он замечает, что сверху срывается лавина шириной $L=100$ м, движущаяся с постоянным ускорением $a=5,0$ м/с$^2$. Человек находится прямо напротив середины фронта лавины на расстоянии $l=100$ м от нее. Чтобы спастись, он начинает ехать с некоторой постоянной скоростью в неизменном направлении.
1. С какой минимальной скоростью $u_{\min}$ должен ехать человек, чтобы не попасть под лавину?
2. Под каким углом к фронту лавины должен двигаться человек, если он двигается со скоростью $u_{\min}$?

Часть С. Черная дыра (2 балла) Космический корабль попадает в черную дыру и начинает падать на нее с начального расстояния $R$ по спирали таким образом, что его радиальная $\vartheta_{r}$ и тангенциальная $\vartheta_{t}$, скорости зависят от расстояния $r$ до центра черной дыры по закону: $\vartheta_{r}=\alpha/r$ и $\vartheta_{t}=\beta r^{2}$, где $\alpha$ и $\beta$ — некоторые известные постоянные величины. Радиальная скорость — это компонента вектора скорости $\vartheta$, направленная к центру черной дыры, а тангенциальная скорость — это компонента , перпендикулярная радиальной.
1. Какой угол составляет вектор скорости $\vartheta$ с направлением на центр черной дыры в момент времени, когда расстояние до центра черной дыры сократилось вдвое и стало равным $R/2$?
2. Сколько времени прошло от начала падения до этого момента времени?

комментарий/решение(1)
Задача №2. Настольный шар (8 баллов)
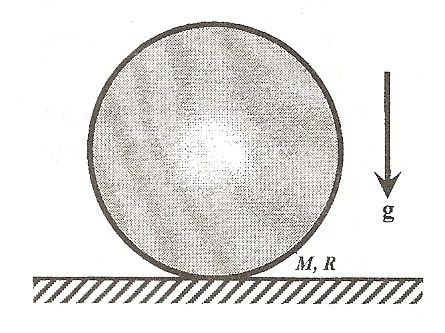
Небольшое тело массой $m$ находится на внутренней поверхности полного шара массой $M$ и радиуса $R$. В начальный момент времени скорости тела и шара равны нулю, а тело находится на высоте от горизонтального стола, равной радиусу шара (см. рис.). Найдите скорости тела и шара в тот момент, когда тело достигнет наинизшей точки. Трение между телом и внутренней поверхностью шара отсутствует. Рассмотрите отдельно два случая:
1) Трение между шаром и столом отсутствует; (3 балла)
2) Шар двигается по столу без проскальзывания. (5 баллов)
Ускорение свободного падения равно $g$.
комментарий/решение
Небольшое тело массой $m$ находится на внутренней поверхности полного шара массой $M$ и радиуса $R$. В начальный момент времени скорости тела и шара равны нулю, а тело находится на высоте от горизонтального стола, равной радиусу шара (см. рис.). Найдите скорости тела и шара в тот момент, когда тело достигнет наинизшей точки. Трение между телом и внутренней поверхностью шара отсутствует. Рассмотрите отдельно два случая:
1) Трение между шаром и столом отсутствует; (3 балла)
2) Шар двигается по столу без проскальзывания. (5 баллов)
Ускорение свободного падения равно $g$.
комментарий/решение
Задача №3. Пираты Карибского моря (6 баллов)
В голливудском приключенческом фильме «Пираты Карибского моря. Сундук мертвеца» два главных героя, капитан Джек Воробей и Уильям Тернер, прошли по дну водоема, используя следующий прием. Они перевернули лодку вверх дном и погрузили ее в воду, а затем использовали запертый воздух для дыхания под водой.
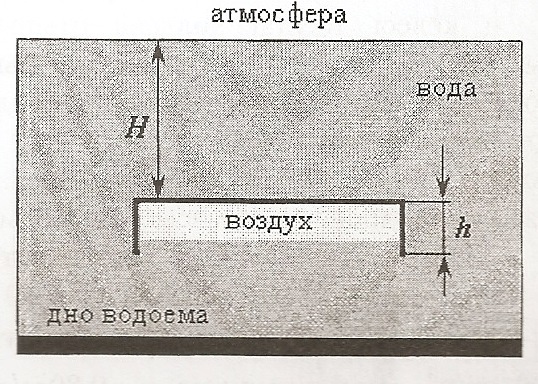
В данной задаче Вам предлагается проанализировать этот метод с физической точки зрения. Будем считать, что лодка прямоугольная, имеет поперечное сечение $S=1.0$ м$^2$, высоту $h=0.50$ м и массу $m=30$ кг. Дно лодки находится на расстоянии $H=10$ м от поверхности воды, плотность воды $\rho_{0} =1000$ кг/м$^3$, средняя плотность тела человека $\rho=1036$ кг/м$^3$, плотность дерева, из которого изготовлена лодка, $\rho_{\sigma}= 700$ кг/м$^3$, ускорение свободного падения $g=9.80$ м/с$^2$, универсальная газовая постоянная $R=8,31$ Дж/(моль$\cdot$К), атмосферное давление $p_{0}=1.01\times 10^{5}$ Па, молярная масса воздуха $\mu=29$ г/моль. Температуру всюду считайте одинаковой и равной $T=293$ К.
1. Найдите силу давления воды на дно лодки; (1.0 балл)
2. Найдите плотность воздуха внутри лодки; (2.0 балла)
3. Какой суммарной массой должны обладать капитан Джек Воробей и Уильям Тернер для того, чтобы они могли идти по дну водоема с такой лодкой? (3 балла)
комментарий/решение
В голливудском приключенческом фильме «Пираты Карибского моря. Сундук мертвеца» два главных героя, капитан Джек Воробей и Уильям Тернер, прошли по дну водоема, используя следующий прием. Они перевернули лодку вверх дном и погрузили ее в воду, а затем использовали запертый воздух для дыхания под водой.
В данной задаче Вам предлагается проанализировать этот метод с физической точки зрения. Будем считать, что лодка прямоугольная, имеет поперечное сечение $S=1.0$ м$^2$, высоту $h=0.50$ м и массу $m=30$ кг. Дно лодки находится на расстоянии $H=10$ м от поверхности воды, плотность воды $\rho_{0} =1000$ кг/м$^3$, средняя плотность тела человека $\rho=1036$ кг/м$^3$, плотность дерева, из которого изготовлена лодка, $\rho_{\sigma}= 700$ кг/м$^3$, ускорение свободного падения $g=9.80$ м/с$^2$, универсальная газовая постоянная $R=8,31$ Дж/(моль$\cdot$К), атмосферное давление $p_{0}=1.01\times 10^{5}$ Па, молярная масса воздуха $\mu=29$ г/моль. Температуру всюду считайте одинаковой и равной $T=293$ К.
1. Найдите силу давления воды на дно лодки; (1.0 балл)
2. Найдите плотность воздуха внутри лодки; (2.0 балла)
3. Какой суммарной массой должны обладать капитан Джек Воробей и Уильям Тернер для того, чтобы они могли идти по дну водоема с такой лодкой? (3 балла)
комментарий/решение
Задача №4. Электрическая дилемма (8 баллов)
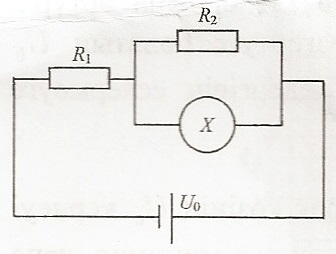
Собрана электрическая схема, показанная на рисунке. Она содержит два постоянных резистора $R_1=3$ Ом и $R_2=1.5$ Ом, а также некоторый съемный элемент $X$, на место которого можно вставлять различные приборы. Вся схема подключена к источнику постоянного напряжения $U_0$, которое можно изменять, а его внутреннее сопротивление пренебрежимо мало.
1. На место элемента $X$ вставляется резистор сопротивлением $R=3$ Ом. Найдите минимальный и максимальный ток через вставленный резистор, если напряжение источника питания $U_0$ меняется от $3$ В до $36$ В; (1 балл)
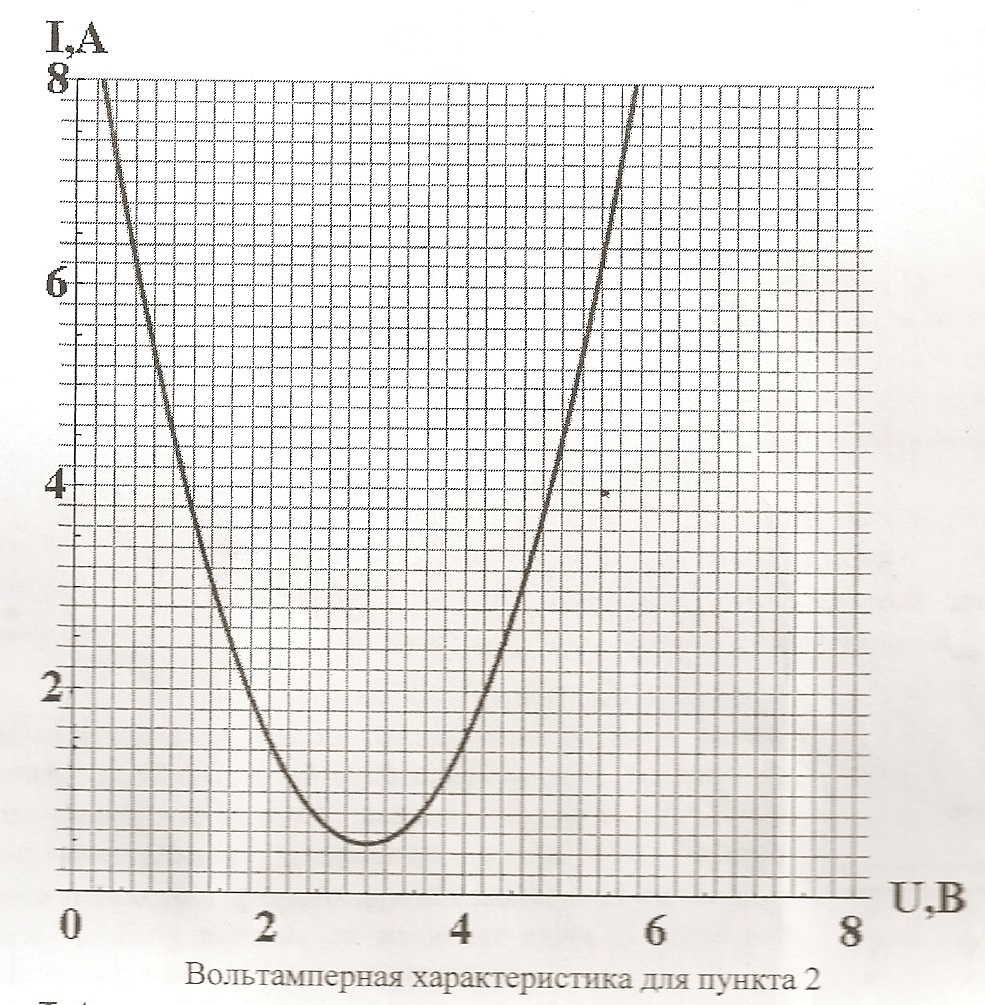
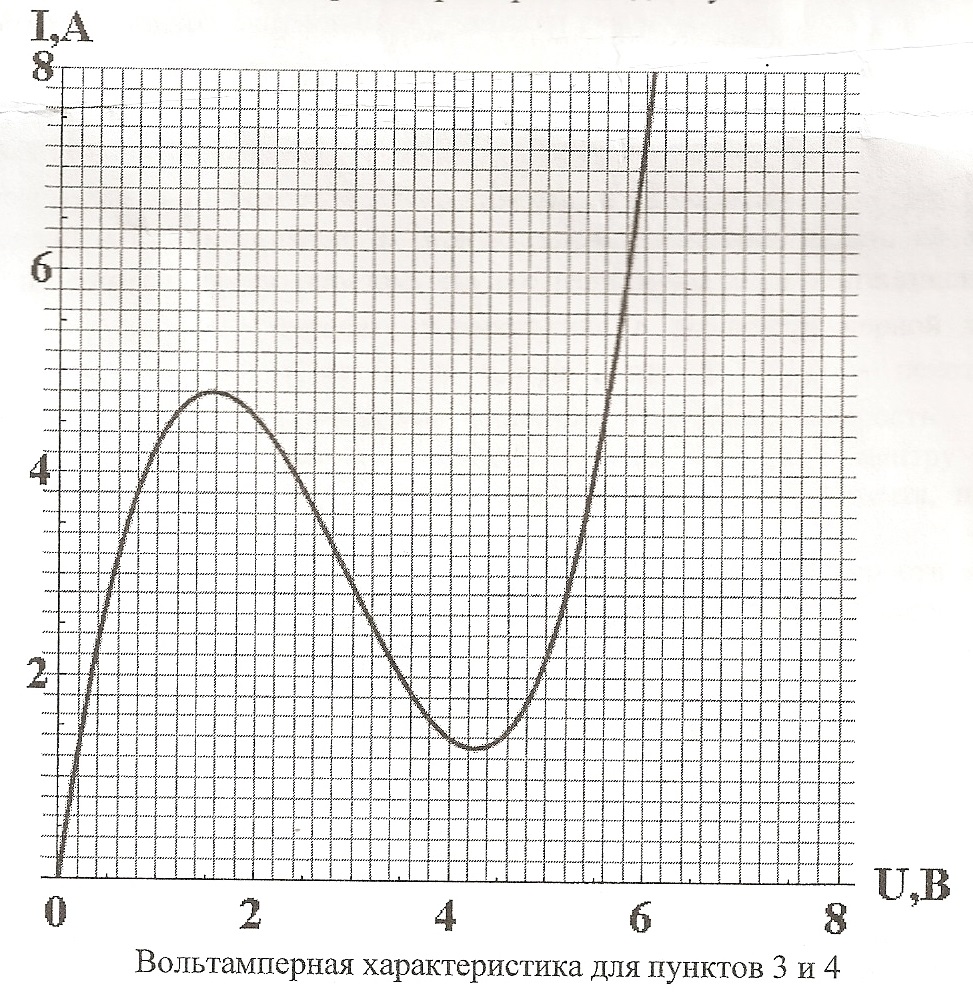
2. На место элемента $X$ вставляется нелинейный элемент, вольтамперная характеристика которого показана на рисунке внизу. Найдите ток через элемент $X$, если напряжение источника питания $U_0=18$ В; (2 балла)
3. На место элемента $X$ вставляется нелинейный элемент, вольтамперная характеристика которого показана на рисунке внизу. Напряжение источника питания $U_0$ увеличивается до $30$ В, а затем обратно уменьшается с $30$ до $0$ В. Постройте на одном графике соответствующие зависимости тока через элемент $X$ от напряжения источника питания $U_0$. (3 балла) $$
комментарий/решение
Собрана электрическая схема, показанная на рисунке. Она содержит два постоянных резистора $R_1=3$ Ом и $R_2=1.5$ Ом, а также некоторый съемный элемент $X$, на место которого можно вставлять различные приборы. Вся схема подключена к источнику постоянного напряжения $U_0$, которое можно изменять, а его внутреннее сопротивление пренебрежимо мало.
1. На место элемента $X$ вставляется резистор сопротивлением $R=3$ Ом. Найдите минимальный и максимальный ток через вставленный резистор, если напряжение источника питания $U_0$ меняется от $3$ В до $36$ В; (1 балл)
2. На место элемента $X$ вставляется нелинейный элемент, вольтамперная характеристика которого показана на рисунке внизу. Найдите ток через элемент $X$, если напряжение источника питания $U_0=18$ В; (2 балла)
3. На место элемента $X$ вставляется нелинейный элемент, вольтамперная характеристика которого показана на рисунке внизу. Напряжение источника питания $U_0$ увеличивается до $30$ В, а затем обратно уменьшается с $30$ до $0$ В. Постройте на одном графике соответствующие зависимости тока через элемент $X$ от напряжения источника питания $U_0$. (3 балла) $$
комментарий/решение