Юниорская олимпиада по математике. Районный этап. 2022-2023 учебный год. 8 класс.
Есеп №1. 5, 8 және 10 тең параллелепипедтің қабырғалары мен биіктігі берілген. Параллелепипедтің диагональін табыңыз.
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) 13
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
A) $3\sqrt{21}$
B) $10\sqrt{3}$
C) 13
D) $9\sqrt{19}$
E) $12\sqrt{2}$
комментарий/решение
Есеп №2. Ребусті шешіңіз: $C,BA+A,AA = B,A.$
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
A) $A=0$, $B=2$, $C=6$
B) $A=5$, $B=3$, $C=8$
C) $A=5$, $B=9$, $C=3$
D) $A=2$, $B=5$, $C=4$
E) $A=0$, $B=1$, $C=7$
комментарий/решение
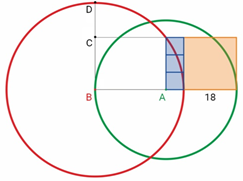
Есеп №3. Төмендегі суретте: Үш көк фигура — шаршылар; Қызғылтсары фигура — қабырғасы 18 шаршы; $A$ нүктесі — жасыл шеңбердің центрі; $B$ нүктесі — қызыл шеңбердің центрі. $CD$ кесіндісінің ұзындығын табыңыз.
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
A) 10
B) 14
C) 18
D) 22
E) 12
комментарий/решение
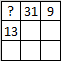
Есеп №4. Сиқырлы $3 \times 3$ шаршы — бағандар, қатар мен екі диагональдағы сандардың қосындысы бір-біріне тең. Төменде сиқырлы шаршы бейнеленгенжәне үш саннан басқа сандарды өшіріп тастаған. Сұрақ белгісінің орнына сай келетін санды табыңыз.
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
A) 14
B) 25
C) 92
D) 12
E) 90
комментарий/решение
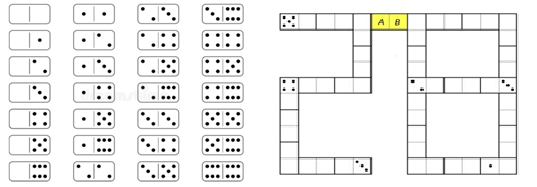
Есеп №5. 28 доминодан құралған жиынтық төмендегідей: Нүкте сандары бірдей доминоның жарты бөлігі бір-біріне тиіп тұратындай етіп 28 домино қойылды. Кейбір доминолардың жартысындағы нүктелерді түгелдей өшіріп тастады. Соңында төмендегідей фигура шықты (кейбір нүктелері жоқ доминоларда басынан бері нүкте болмауы мүмкін). $A$ бөлігіндегі нүктелер саны: $\ldots$. $B$ бөлігіндегі нүктелер саны: $\ldots$.
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
A) $A=2, B=4$
B) $A=5, B=6$
C) $A=8, B=2$
D) $A=5, B=2$
E) $A=2, B=5$
комментарий/решение
Есеп №6. $p+25$ жай санның жетінші дәрежесі болатындай жай сан $p$ таңдалған. $p$ қандай сандарға тең бола алады?
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
A) 771
B) 299
C) 103
D) 527
E) 1307
комментарий/решение
Есеп №7. Доғал үшбұрыш $ABC$-ның $C$ бұрышы доғал. $\angle ACP = CPQ = 90^\circ$ болатындай $AB$ және $BC$ қабырғаларында $P$ мен $Q$ нүктелері алынған. $AC = 25$, $CP = 20$, $\angle APC =\angle A+\angle B$ екені белгілі болса $PQ$ кесіндісі неге тең екенін табыңыз.
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
A) 12
B) 16
C) 20
D) 42
E) 17
комментарий/решение
Есеп №8. Өрнекті ықшамдаңыз: $x^4+7x^3-21x^2-27x.$
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
A) $(x-1)(x-2)(x+7)x$
B) $(x+1)(x-3)(x+9)$
C) $(x+1)(x-3)(x+9)x$
D) $(x-1)(x+3)(x+9)x$
E) $(x+3)(x-1)(x+9)$
комментарий/решение
Есеп №9. Натурал тақ $n$ санның үш әртүрлі натурал бөлгіштерінің қосындысы 10327 тең. Ең кіші $n$ мәні нешеге тең?
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
A) 10327
B) 15633
C) 8725
D) 6735
E) 9817
комментарий/решение
Есеп №10. $\omega$ шеңберінің $AC$ диаметрінің екі жағында $B$ және $D$ нүктелері орналасқан. $AB = 3\sqrt{6}$, $CD = 3$ екені белгілі, ал $ABC$ үшбұрышының ауданы $BCD$ үшбұрышының ауданынан үш есе үлкен. $\omega$ шеңберінің радиус табыңыз.
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
A) 7
B) 9
C) 3,5
D) 5
E) 4,5
комментарий/решение
Есеп №11. $a$ және $b$ оң сандарының көбейтіндісі 1 тең. $(3a+2b)(3b+2a) = 295$ өрнек берілген болса $a+b$ нешеге тең?
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
A) 45
B) 12
C) 4
D) 7
E) 47
комментарий/решение
Есеп №12. Теңбұрышты үшбұрыш $ABC$-ның $AC$ қабырғасында $D$ нүктесі белгіленген. $AD$ және $DC$ кесінділерінде бастапқы үшбұрыштан сырттай $ADE$ мен $DCF$ теңбұрышты үшбұрыштар құралды. $DEF$-тің периметрі 19-ға, ал $ABCFE$ бесбұрышының периметрі 43-ке тең. $AB$ мен $ЕF$ кесінділерінің ұзындықтарын табыңыз.
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
A) 12, 5
B) 15, 12
C) 12, 7
D) 7, 15
E) 7, 12
комментарий/решение
Есеп №13. Топта кейбір адамдар бір бірінен дос (егер $A$ $B$-мен дос болса, $B$ да $A$-мен дос). Әрбір 100 адамның ішінде бір-бірімен дос жұптардың саны тақекен. Осы топта мүмкін бола алатын ең үлкен адамдар санын табыңыз.
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
A) 422
B) 263
C) 141
D) 101
E) 100
комментарий/решение
Есеп №14. Көбейткіштерге жіктеңіз: $2x^4-2x^2-24.$
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
A) $(x-2)(x^2+3)(2x+4)$
B) $(x+2)(x+3)(2x-4)$
C) $(x-2)(x^4+3)(2x-4)$
D) $(x-3)(3x-2)(x^3+1)$
E) $(x+2)(x+3)(2x+4)$
комментарий/решение
Есеп №15. $x$ және $y$ сандары $\frac{3x+y}{x-3y}=-2$ болатындай нөлдік емес нақты сандар. $\frac{x+3y}{3x-y}$ өрнегінің мәнін табыңыз.
A) $-1$
B) $-3$
C) 1
D) 2
E) 3
комментарий/решение
A) $-1$
B) $-3$
C) 1
D) 2
E) 3
комментарий/решение
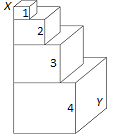
Есеп №16. Қабырғалары 1, 2, 3 және 4 болатын текшелер төменде көрсетілгендей орналасқан. Ұзындығы 3-ке тең текшенің бойымен өткен $XY$ бөлігінің ұзындығын табыңыз.
A) $3\sqrt{33}:5$
B) $2\sqrt{3}$
C) $2\sqrt{33}:3$
D) 4
E) $3\sqrt{2}$
комментарий/решение
A) $3\sqrt{33}:5$
B) $2\sqrt{3}$
C) $2\sqrt{33}:3$
D) 4
E) $3\sqrt{2}$
комментарий/решение
Есеп №17. Есептеңіз: $\frac{2^3+2^3}{2^{-3}+2^{-3}}.$
A) 16
B) 24
C) 32
D) 48
E) 64
комментарий/решение
A) 16
B) 24
C) 32
D) 48
E) 64
комментарий/решение
Есеп №18. Балақай әкесімен бірге тирге барады. Әкесі оған 10 оқ алып береді. Әкесі баласы нысанаға тигізгені үшін тағы да 1 оқ беріп қиыс кеткен кезінде 1 алып отырды. Соңында балақай 55 рет атқаны белгілі болады. Ол неше рет тигізді?
A) 42
B) 55
C) 50
D) 60
E) 65
комментарий/решение
A) 42
B) 55
C) 50
D) 60
E) 65
комментарий/решение
Есеп №19. 19-ға бөлінетін әрі 19-бен аяқталатын қанша төрт таңбалы сан бар?
A) 24
B) 5
C) 0
D) 1
E) 43
комментарий/решение
A) 24
B) 5
C) 0
D) 1
E) 43
комментарий/решение
Есеп №20. Қанша бес таңбалы санды цифрларының орынын ауыстыру арқылы палиндромға айналдыра аламыз? (Палиндром-оңнан солға, солдан оңға бірдей оқылатын сан.)
A) 1000
B) 100
C) 500
D) 900
E) 750
комментарий/решение
A) 1000
B) 100
C) 500
D) 900
E) 750
комментарий/решение
Есеп №21. $5^{867}$ саны $2^{2013}$ мен $2^{2014}$ арасында орналасқан. $1\le m \le 2012$, $5^n < 2^m < 2^{m+2} < 5^{n+1}$ шарттарға бағынатын қанша $(m, n)$ жұптары бар?
A) 278
B) 279
C) 280
D) 281
E) 282
комментарий/решение
A) 278
B) 279
C) 280
D) 281
E) 282
комментарий/решение
Есеп №22. Екі санның қосындысы айырмасынан 5 есе үлкен. Үлкен санның кішкентай санға қатынасын табыңыз.
A) $5:4$
B) $3:2$
C) $9:5$
D) $2:1$
E) $5:2$
комментарий/решение
A) $5:4$
B) $3:2$
C) $9:5$
D) $2:1$
E) $5:2$
комментарий/решение
Есеп №23. Соңғы цифрін табыңыз: $2023^{2023}+2^{2023}+3^{2023}.$
A) 7
B) 0
C) 1
D) 2
E) 5
комментарий/решение
A) 7
B) 0
C) 1
D) 2
E) 5
комментарий/решение
Есеп №24. $BD$ — $ABC$ үшбырышының биссектрисасы, $AD = 3$ және $DC = 8$. $ABC$ үшбұрышының периметрінің мүмкін ең кіші мәнін табыңыз.
A) 30
B) 33
C) 35
D) 36
E) 37
комментарий/решение
A) 30
B) 33
C) 35
D) 36
E) 37
комментарий/решение
Есеп №25. $8 \times 8$ тақтада қабырғасы бойынша тұрған көршісінен айырмашылығы 1 болатындай 1-ден 64-ке дейін натурал сандар жазылған. Сол жақ төменгі бұрыштан оң жаққа дейін сандардың қосындысы ең кіші нешеге тең бола алады?
A) 8
B) 121
C) 50
D) 88
E) 64
комментарий/решение
A) 8
B) 121
C) 50
D) 88
E) 64
комментарий/решение
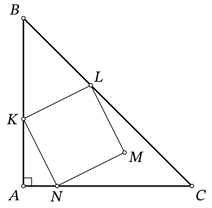
Есеп №26. $A$ бұрышы тік бұрыш $ABC$ үшбырышы берілген. $KLMN$ шаршысы суреттегідей орналасқан: $K, L, N$ нүктелері $AB, BC, AC$ қабырғаларында жатыр, ал $M$ нүктесі $ABC$ үшбұрышының ішінде жатыр. $AK = 7$, $AN = 3$ белгілі болса $AC$ кесіндісінің ұзындығын табыңыз.
A) 15
B) 17
C) 23
D) 25
E) 9
комментарий/решение
A) 15
B) 17
C) 23
D) 25
E) 9
комментарий/решение
Есеп №27. $N$ натурал санының балық бөлгіштерін жазып әр бөлгіштің цифрларының қосындысы жазылды да осы сандардың ішінде 1-ден 9-ға дейін барлық сандар бар екені анық болды. $N$-нің ең кіші мәнін табыңыз.
A) 144
B) 288
C) 346
D) 502
E) 998
комментарий/решение
A) 144
B) 288
C) 346
D) 502
E) 998
комментарий/решение
Есеп №28. $ABC$ үшбұрышының тік бұрышынан түскен $CH$ биіктігі $BL$ биссектриасасын екіге бөледі. $BAC$ бұрышының мәнін табыңыз.
A) 90
B) 60
C) 45
D) 30
E) 70
комментарий/решение
A) 90
B) 60
C) 45
D) 30
E) 70
комментарий/решение
Есеп №29. $M$ мен $N$ нүктелері $ABCD$ төртбұрышының $BC$ және $AD$ қабырғаларының орталары. $\angle В = 150\circ$, $\angle С = 90\circ$ және $AB = CD$ екені белгілі болса $MN$ және $BC$ түзулері қиылысатын бұрыштың мәнін табыңыз.
A) 40
B) 30
C) 55
D) 45
E) 60
комментарий/решение
A) 40
B) 30
C) 55
D) 45
E) 60
комментарий/решение
Есеп №30. $a^2+b = b^2+c = c^2+a$ белгілі болса, төмендегі $(a^2-b^2)+b(b^2-c^2)+c(c^2-a^2)$ өрнектің қандай мәндері бола алады?
A) 0
B) 1
C) 2
D) 5
E) 10
комментарий/решение
A) 0
B) 1
C) 2
D) 5
E) 10
комментарий/решение