11-я международная Иранская олимпиада по геометрии, 2023 год, третья лига, 11-12 классы

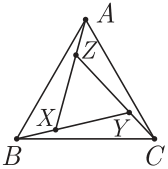
Есеп №1. Суретте теңқабырғалы

$ABC$ үшбұрышы аудандары бірдей 4 үшбұрышқа бөлінген.

$ABX$ ,

$BCY$ ,

$CAZ$ үшбұрыштары өзара тең, ал төртінші

$\triangle XYZ$ — теңқабырғалы үшбұрыш.

$X, Y, Z$ нүктелері

$ABC$ үшбұрышына іштей сызылған шеңбердің бойында жатқанын дәлелдеңіз.

комментарий/решение(1)

Есеп №2. Іштей сызылған

$ABCD$ төртбұрышының

$CD$ қабырғасында

$\angle CBP = 90^\circ$ болатындай

$P$ нүктесі алынған.

$AC$ және

$BP$ түзулері

$K$ нүктесінде қиылысады, және сол нүкте үшін

$AK = AP = AD$ теңдігі орындалады.

$H$ арқылы

$B$ нүктесінен

$AC$ түзуіне түсірілген перпендикуляр табанын белгілейік.

$\angle APH = 90^\circ$ екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №3.

$ABC$ үшбұрышында

$I$ ,

$I_A$ ,

$I_C$ нүктелері, сәйкесінше, іштей сызылған,

$A$ -ға қарсы орналасқан іштейсырт,

$C$ -ға қарсы орналасқан іштейсырт шеңберлердің центрлері болсын.

$AD$ —

$\triangle ABC$ -ның биіктігі болсын.

$BDI_C$ үшбұрышына сырттай сызылған шеңберді

$BI$ және

$DI_A$ түзулері екінші рет, сәйкесінше,

$P$ және

$Q$ нүктелерінде қияды.

$AP = AQ$ екенін дәлелдеңіз. (

$ABC$ үшбұрышында

$A$ -ға қарсы орналасқан іштейсырт шеңбер деп,

$BC$ кесіндісін және

$AB$ мен

$AC$ қабырғаларының сөзындыларын жанайтын шеңберді айтамыз.)
комментарий/решение(1)

Есеп №4. Сүйірбұрышты

$ABC$ үшбұрышының ішінде

$\angle BPC = 90^\circ$ және

$\angle BAP = \angle PAC$ болатындай

$P$ нүктесі алынған.

$D$ арқылы

$P$ нүктесінің

$BC$ қабырғасына түсірілген проекциясын белгілейік.

$M$ және

$N$ нүктелері, сәйкесінше,

$\triangle ABD$ және

$\triangle ADC$ -ға іштей сызылған шеңберлердің центрлері болсын.

$BMNC$ іштей сызылған төртбұрыш екенін дәлелдеңіз.
комментарий/решение(1)

Есеп №5.

$\omega$ шеңберіне

$ABCD$ төртбұрышы іштей сызылған.

$E$ нүктесі

$AC$ кесіндісіндегі тұрақты нүкте болсын.

$M$ нүктесі

$\omega$ бойындағы кез келген нүкте.

$AM$ және

$BD$ түзулері

$P$ нүктесінде қиылысады.

$EP$ түзуі

$AB$ және

$AD$ түзулерін, сәйкесінше,

$R$ және

$Q$ нүктелерінде қияды.

$BQ$ және

$DR$ түзулері

$S$ , ал

$MS$ және

$AC$ түзулері

$T$ нүктесінде қиылысады.

$M$ нүктесінің таңдауына қарамастан,

$CMT$ үшбұрышына сырттай сызылған шеңбер

$C$ -дан өзгеше тұрақты нүкте арқылы өтетінін дәлелдеңіз.
комментарий/решение