11-я международная Иранская олимпиада по геометрии, 2023 год, третья лига, 11-12 классы

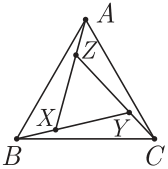
Задача №1. На рисунке ниже равносторонний треугольник

$ABC$ разделён на 4 треугольника равных площадей; три из них — это равные треугольники

$ABX$ ,

$BCY$ ,

$CAZ$ , а четвёртый, меньший, — это равносторонний треугольник

$XYZ$ . Докажите, что точки

$X, Y, Z$ лежат на вписанной окружности треугольника

$ABC$ .

комментарий/решение(1)

Задача №2. Точка

$P$ лежит на стороне

$CD$ вписанного четырёхугольника

$ABCD$ так, что

$\angle CBP = 90^\circ$ . Прямые

$AC$ и

$BP$ пересекаются в точке

$K$ , при этом

$AK = AP = AD$ . Пусть

$H$ — это проекция точки

$B$ на прямую

$AC$ . Докажите, что

$\angle APH = 90^\circ$ .
комментарий/решение(1)

Задача №3. В треугольнике

$ABC$ точки

$I$ ,

$I_A$ и

$I_C$ — это центр вписанной окружности, центр вневписанной окружности при вершине

$A$ и центр вневписанной окружности при вершине

$C$ соответственно. Пусть

$AD$ — высота

$\triangle ABC$ . Прямые

$BI$ и

$DI_A$ во второй раз пересекают описанную окружность треугольника

$BDI_C$ соответственно в точках

$P$ и

$Q$ . Докажите, что

$AP = AQ$ . (Вневписанной окружностью при вершине

$A$ треугольника

$ABC$ называется окружность, которая касается отрезка

$BC$ и продолжений сторон

$AB$ и

$AC$ .)
комментарий/решение(1)

Задача №4. Точка

$P$ лежит внутри остроугольного треугольника

$ABC$ так, что

$\angle BPC = 90^\circ$ и

$\angle BAP = \angle PAC$ . Пусть

$D$ — проекция точки

$P$ на сторону

$BC$ . Пусть

$M$ и

$N$ — это центры вписанных окружностей треугольников

$ABD$ и

$ADC$ соответственно. Докажите, что четырёхугольник

$BMNC$ является вписанным.
комментарий/решение(1)

Задача №5. В окружность

$\omega$ вписан четырёхугольник

$ABCD$ . Пусть

$E$ — фиксированная точка на отрезке

$AC$ . Точка

$M$ — это произвольная точка на

$\omega$ , а прямые

$AM$ и

$BD$ пересекаются в точке

$P$ . Прямая

$EP$ пересекает стороны

$AB$ и

$AD$ в точках

$R$ и

$Q$ соответственно, прямых

$BQ$ и

$DR$ пересекаются в точке

$S$ , а прямые

$MS$ и

$AC$ пересекаются в точке

$T$ . Докажите, что независимо от выбора точки

$M$ , описанная окружность треугольника

$CMT$ проходит через фиксированную точку, отличной от

$C$ .
комментарий/решение