7-я олимпиада им. Шалтая Смагулова, 6 класс, 3 тур

Есеп №1. Келесі теңдік орындалатындай етіп, алты жұлдызшаны нөлден өзге алты түрлі цифрларға ауыстырыңыз: $$(**+*)\cdot(**+*)=2024.$$
комментарий/решение

---

Есеп №2. 18 бала олимпиадалық резерв мектебіне қабылдау тестін жазды. Балаларға түрлі нұсқалар берілді, түрлі нұсқада түрлі тапсырмалар бар, бірақ әр нұсқада тапсырмалар саны тең болған. Тестті тексергеннен кейін, бірнеше оқушы өзіне ұсынылған есептердің тек $\frac{1}{2}$-ін, тағы бірнешеуі тек $\frac{1}{3}$-ін шешкені, ал қалғандары — бірде-бір есеп шешпегені белгілі болды. Сондай-ақ барлық оқушылар барлық есептердің тек $\frac{1}{9}$-ін ғана шешкен. Қанша бала бірде-бір есепті шеше алмады?
комментарий/решение

---

Есеп №3. Натурал $n$ санының ең кіші үш бөлгішінің қосындысы 8-ге тең. $n$ санының соңғы екі цифры қандай болуы мүмкін?
комментарий/решение

---

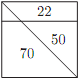
Есеп №4. Шаршы көлденең сызық пен диагональ арқылы төрт бөлікке бөлінген. Олардың үшеуінің ауданы Суретте көрсетілген.
   a) Төртінші бөліктің ауданын табыңыз.
   б) Шаршының диагоналы горизонталь түзуді қандай қатынаста бөледі?

комментарий/решение

---

Есеп №5. Сыныпта 30 оқушы бар, оның бірі — Вася. Васяның сыныптастарының әрқайсысының Васямен тура 5 ортақ досы бар. Сыныпта достарының саны тақ оқушы бар екенін дәлелдеңіз.
комментарий/решение

---