7-я олимпиада им. Шалтая Смагулова, 6 класс, 3 тур

Задача №1. Замените шесть звездочек шестью различными ненулевыми цифрами так, чтобы выполнялось равенство: $$(**+*)\cdot(**+*)=2024.$$
комментарий/решение

Задача №2. 18 детей писали вступительный тест в школу олимпийского резерва. Детям дали разные варианты, в разных вариантах — разные задачи, но в каждом варианте одинаковое количество задач. После поверки теста оказалось, что несколько учеников решили только $\frac{1}{2}$ предлагавшихся им задач, еще несколько — только $\frac{1}{3}$, остальные же ни одну задачу не решили. Также известно, что всеми учениками решены только $\frac{1}{9}$ всех задач. Сколько детей не решили ни одну задачу?
комментарий/решение

Задача №3. Известно, что сумма трех наименьших делителей натурального числа $n$ равна 8. Какими могут быть две последние цифры числа $n$?
комментарий/решение

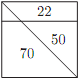
Задача №4. Квадрат разделен горизонтальной прямой и диагональю на четыре части. Площади трех из них указаны на рисунке.
а) Найдите площадь четвертой части.
б) В каком отношении делит диагональ квадрата горизонтальную линию?

комментарий/решение

Задача №5. В классе 30 учеников, один из них — Вася. Каждый из Васиных одноклассников имеет ровно 5 общих друзей с Васей. Докажите, что в классе есть ученик с нечетным числом друзей.
комментарий/решение