7-я олимпиада им. Шалтая Смагулова, 6 класс, 1 тур

Задача №1. Сумма возрастов всех детей в классе равна 187 годам, а два года назад эта сумма равнялась 143 годам. Сколько детей учится в классе?
комментарий/решение

Задача №2. Асан тратит половину своей зарплаты на еду. Через год его зарплата увеличилась на 10 процентов, а цены на продукты выросли на 21 процент. Какой процент зарплаты теперь Асан будет тратить на еду?
комментарий/решение(1)

Задача №3. Вычислите: $11,\!111111:1,\!111+1111,\!1111:11,\!11+111111,\!11:111,\!1-0,\!111.$
комментарий/решение

Задача №4. Вычислите: $99 + 199 + 299 + 399 + \ldots +1899+ 1999$.
комментарий/решение(1)

Задача №5. Даны 100 натуральных чисел. Каждое число делится либо на 2, либо на 3. Среди них ровно 70 делятся на два, и ровно 48 — на три. Сколько из них делятся на 6?
комментарий/решение(1)

Задача №6. На рисунке квадрат с площадью 81 см$^2$ согнули по прямой. Скольким сантиметрам равна сумма периметров, полученных четырех закрашенных треугольников?

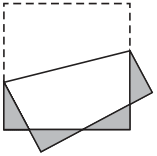
комментарий/решение(1)

Задача №7. Покупатель купил у Армана товар на сумму 500 тенге и дал ему одну купюру в 1000 тенге. У Армана не нашлось сдачи. Он разменял 1000 тенге у соседа, а затем дал сдачу покупателю. Через некоторое время вернулся сосед и сообщил Арману, что та купюра в 1000 тенге — фальшивая, и Арману пришлось вернуть эти 1000 тенге обратно. Сколько денег потерял Арман в итоге?
комментарий/решение

Задача №8. В квадрат $ABCD$ со стороной 50 во внутренную сторону вписаны две полуокружности с диаметрами $AB$ и $AD$ (см. рис.). Найдите площадь заштрихованной части квадрата. Считайте, что $\pi = 3,\!14$.

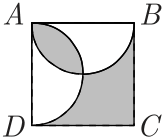
комментарий/решение

Задача №9. Вычислите сумму: $\left[ \frac{1}{4} \right]+\left[ \frac{2}{4} \right]+\left[ \frac{3}{4} \right]+\ldots +\left[ \frac{99}{4} \right]+\left[ \frac{100}{4} \right].$ (Через $\left[ a \right]$ обозначена целая часть числа $a$, то есть это наибольшее целое число, не превосходящее $a$. Например, $\left[0,\!75 \right]=0$, $\left[3,\!56 \right]=3$, $\left[ 4 \right]=4$.)
комментарий/решение

Задача №10. На планету Земля прилетели несколько инопланетян. После этого каждый стал выбирать своим днем рождения один из двенадцати месяцев. Они обнаружили, что независимо от того, какие месяцы они не выбирали, то найдутся по крайней мере четыре, которые отмечали свои дни рождения в одном и том же месяце. Какое наименьшее число инопланетян прибыло на Землю?
комментарий/решение

Задача №11. Натуральное число назовём число «красивым», если оно имеет ровно три натуральных делителя (включая единицу и само число). Найдите сумму пяти наименьших красивых чисел.
комментарий/решение

Задача №12. Найдите наименьшее натуральное число, кратное 7, сумма цифр которого равна 22.
комментарий/решение

Задача №13. Найдите наименьшее натуральное число $n$ такое, что $n!$ делится на 2024. (Как обычно, $n!$ означает произведение всех натуральных чисел от 1 до $n$, то есть $n!=1\cdot 2\cdot \ldots \cdot n$.)
комментарий/решение

Задача №14. На рисунке даны две окружности диметров 3 и 4 с общим центром в точке $O$. Длина выделенной дуги $AB$ в $1,\!25$ раза меньше длины выделенной дуги $CD$. Известно, что $\angle XOA=30^\circ$. Скольким градусам равен $\angle DOC$?

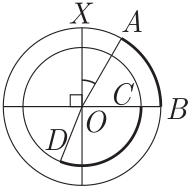
комментарий/решение

Задача №15. На рисунке дана фигура. Каждая сторона фигуры равна 1, а каждый угол равен $60^\circ$ или $240^\circ$. Эту фигуру поностью разбили на маленькие треугольники, стороны каждого из которых равны 1. Сколько треугольников получится при таком разбиении?

комментарий/решение

Задача №16. Если цифры пятизначного числа, записываемого различными цифрами, записать в обратном порядке, то полученное число будет в 4 раза больше исходного. Чему равна сумма цифр исходного числа?
комментарий/решение

Задача №17. Даны четыре последовательных натуральных числа. Произведение двух больших из них на 4450 больше произведения двух меньших. Чему равно наименьшее из данных четырех чисел?
комментарий/решение

Задача №18. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась втрое, то общий доход семьи вырос бы на $120\%$. Если бы стипендия дочери уменьшилась в два раза, общий доход семьи сократился бы на $3\%$. Сколько процентов от общего дохода семьи составляет зарплата жены?
комментарий/решение

Задача №19. Дана последовательность чисел: 2024, 2032, 2039, 2053, 2063, ?. Определив закономерность в последовательности, найдите число, которое должно стоять на месте вопросительного знака.
комментарий/решение

Задача №20. На рисунке дан квадрат размера $n \times n$, все клетки которого заполнены (по некоторому правилу) числами 1, 2, 3, $\ldots$, $n^2$. Известно, что на пересечении двух главных диагоналей квадрата стоит число $A=1013$. Найдите число $n$.

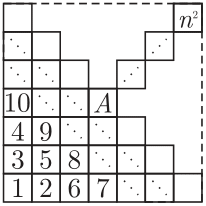
комментарий/решение