Областная олимпиада по математике, 2021 год, 10 класс
Комментарий/решение:
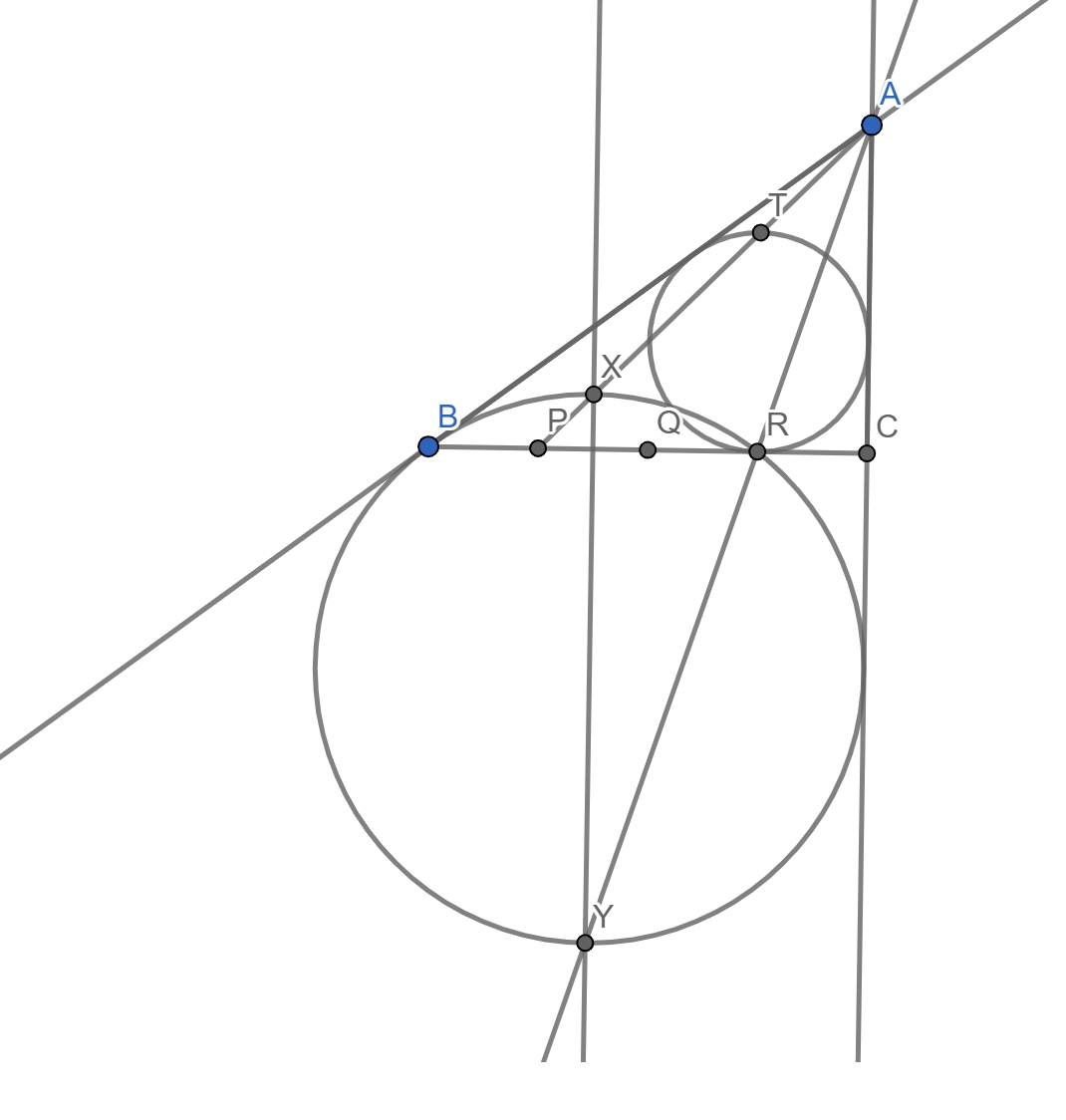
Пусть окружность, вписанная в $\triangle ABC$ касается $BC$ в $R`$.
Тогда $CR` = p - AB \Leftrightarrow CR` = \frac{AB+AC+BC}{2} - AB = \frac{AC+BC-AB}{2} = \frac{BC}{4} = CR$
Отсюда, точки $R$ и $R`$ совпадают, и соответсвенно, $P$ - симметричная $R$, является точкой касания вневписанной окружности $\triangle ABC$.
Рассмотрим окружность, касающуюся $AB$ в $B$. ($\omega_1$)
Легко доказать следующую Лемму (Лемма 1):
$\cdot$ Если P - точка касания вневписанной окружности напротив А, R - точка касания вписанной окружности с BC, T - точка пересечения AP с вписанной окружностью, то $RT$ - диаметр вписанной окружности.
Обозначим точку T также как и в лемме. Тогда $RT \parallel XY$ - сер. перу к $PQ$
Тогда при гомотетии с коэффициентом $AY/AR$ из $A$, вписанная окружность перейдет в $\omega_1$ и по Лемме 1 , XY - ее диаметр. Легко заметить, что $\omega_1$ и есть искомая окружность, что завершает доказательство.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.