Областная олимпиада по математике, 2001 год, 10 класс

Четырехугольник $ABCD$ вписан в окружность с диаметром $BD$. Пусть $F$ симметрично $A$ относительно $BD$, а $N$ — точка пересечения $AF$ и $BD$. Прямая, проходящая через $N$ и параллельно $AC$, пересекается с прямыми $CD$ и $BC$ в точках $P$ и $Q$, соответственно. Докажите, что точки $P$, $C$, $Q$ и $F$ — вершины прямоугольника.

Комментарий/решение

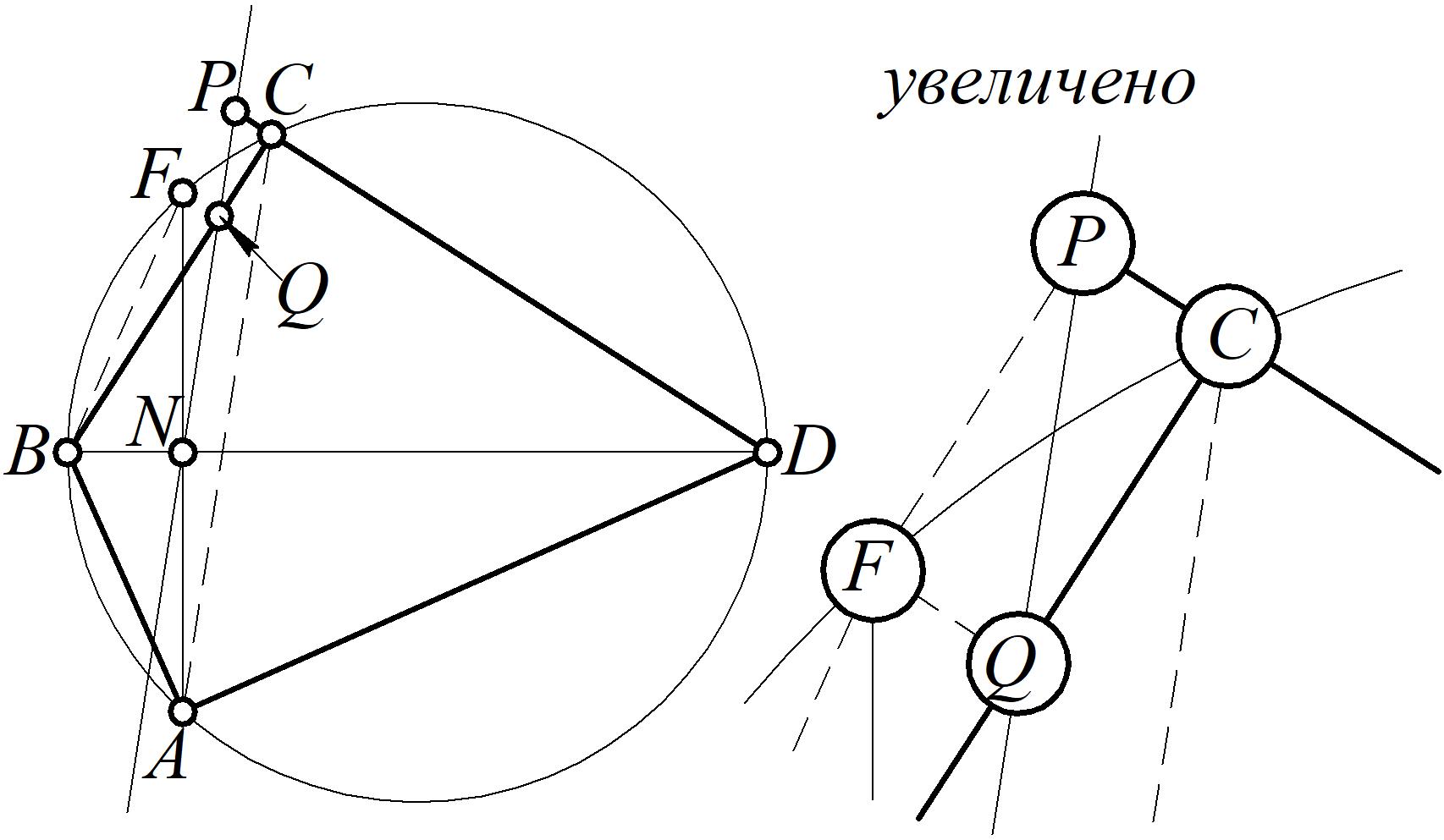
Пусть $O$-точка пересечения диагоналей $CQFD $.Учитывая, что $ABCD $-вписаный, и то, что $\angle BAD $ и $\angle BCD $ опираются на диаметр, получаем, что $\angle BAD =\angle BCD =90^\circ$. $\triangle FND =\triangle AND $ по двум сторонам и 1 углу. Из этого следует , что дуги $FD,AD $ равны. $\angle FCD =\angle DCA $ так как опираются на равные дуги. Учитывая, что по условию $NQ||AC $, получим $\angle PCA =\angle CPQ =\angle FCD $ как внутренние накрест лежащие при параллельных. Из этого следует, что $\triangle COP $-равнобедренный. $CO=OP $. $\angle QCO =90-\angle FCD$; $\angle CQP =90-\angle QPC= 90^\circ-\angle FCD $ из этого $\triangle COQ $ равнобедренный. Следовательно $QO=OP =CO $.Вспомним, что $ NQ ||AC $. По теореме Фалеса получим $CO=OF $. Таким образом $CQFD $-4х угольник в котором диагонали равны и делят друг друга пополам, то есть прямоугольник

что такое H?

Это опечатка. Вместо $H$ следует понимать $N$

Очень благодарен за ревью моего решения, Куаныш!