11-я Жаутыковская олимпиада (2015), теоретический тур
(7 баллов)
Для решения каждой части используйте специальные, выданные вам бланки, на которых выполните требуемые построения.
Описание этих построений, а также расчеты проведите на этих же бланках.
Задача 1.1 (2.0 балла)
Задача 1.2 (2.0 балла)
Задача 1.3 (3.0 балла)
посмотреть в олимпиаде
Задача 1.1 (2.0 балла)
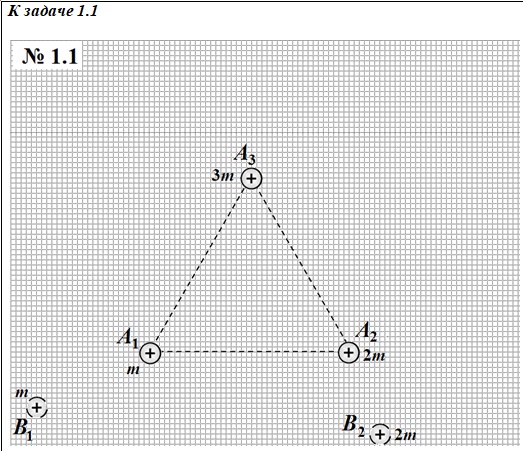
Задача 1.2 (2.0 балла)
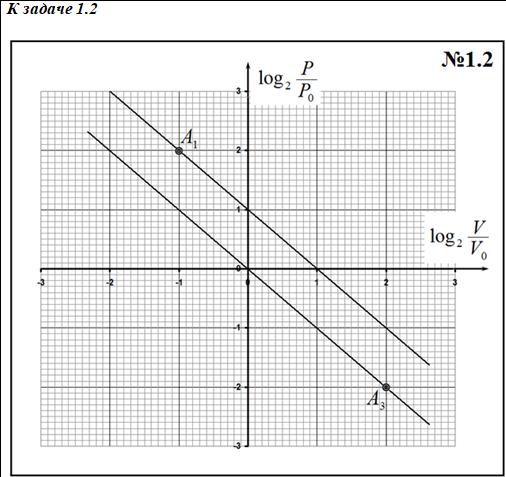
Задача 1.3 (3.0 балла)
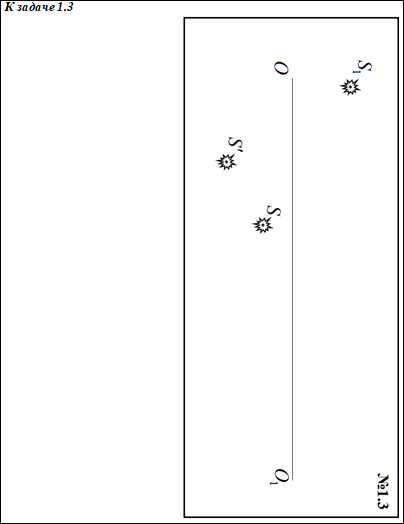
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.