11-я Жаутыковская олимпиада (2015), теоретический тур
Задача №1. (7 баллов)
Для решения каждой части используйте специальные, выданные вам бланки, на которых выполните требуемые построения. Описание этих построений, а также расчеты проведите на этих же бланках.
Задача 1.1 (2.0 балла)
Задача 1.2 (2.0 балла)
Задача 1.3 (3.0 балла)
комментарий/решение
Для решения каждой части используйте специальные, выданные вам бланки, на которых выполните требуемые построения. Описание этих построений, а также расчеты проведите на этих же бланках.
Задача 1.1 (2.0 балла)
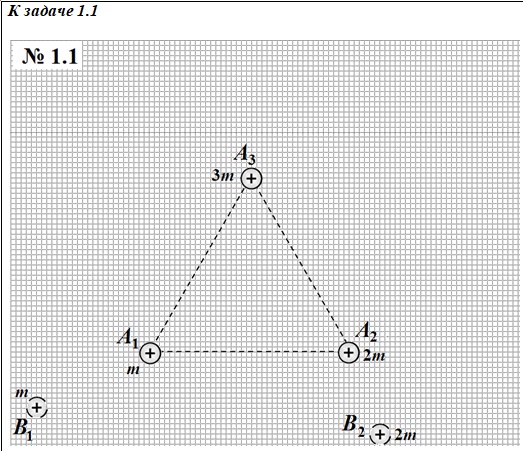
Задача 1.2 (2.0 балла)
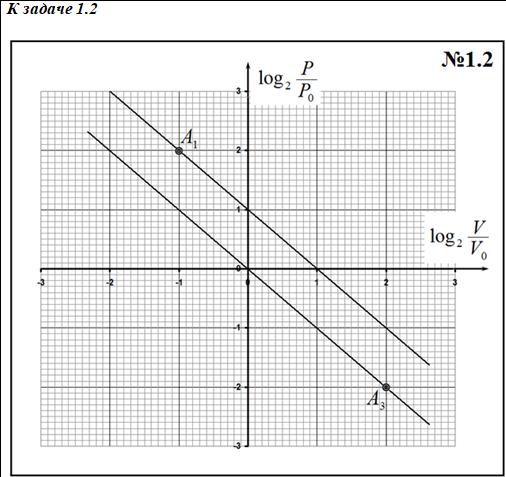
Задача 1.3 (3.0 балла)
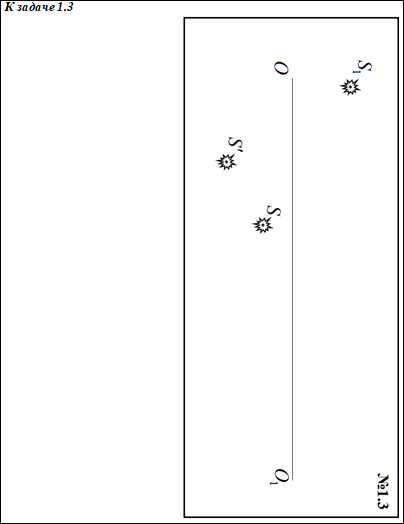
комментарий/решение
Задача №2. Сосуд с водой (7 баллов)
1. [2,0 балла] Найдите высоту уровня воды в сосуде $x=x_0$ в тот момент, когда трубка будет полностью заполнена водой. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$ и найдите его численное значение. Стенки сосуда и трубки покрывают материалом, который не проводит тепло. Воздуху внутри сосуда начинают сообщать тепло достаточно быстро, так что вода не успевает прогреваться.
2. [0,5 балла] Найдите зависимость давления воздуха в сосуде $p(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
3. [1,0 балла] Найдите зависимость температуры воздуха в сосуде $T(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
4. [1,0 балла] Найдите до какой температуры $T_m$ необходимо нагреть воздух, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $T_0$ и найдите его численное значение.
5. [2,5 балла] Найдите количество теплоты $Q$, которое надо сообщить воздуху, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$, $S$ и найдите его численное значение.
комментарий/решение
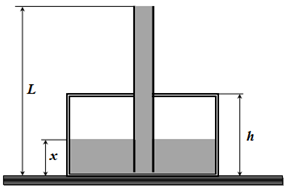
1. [2,0 балла] Найдите высоту уровня воды в сосуде $x=x_0$ в тот момент, когда трубка будет полностью заполнена водой. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$ и найдите его численное значение. Стенки сосуда и трубки покрывают материалом, который не проводит тепло. Воздуху внутри сосуда начинают сообщать тепло достаточно быстро, так что вода не успевает прогреваться.
2. [0,5 балла] Найдите зависимость давления воздуха в сосуде $p(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
3. [1,0 балла] Найдите зависимость температуры воздуха в сосуде $T(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
4. [1,0 балла] Найдите до какой температуры $T_m$ необходимо нагреть воздух, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $T_0$ и найдите его численное значение.
5. [2,5 балла] Найдите количество теплоты $Q$, которое надо сообщить воздуху, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$, $S$ и найдите его численное значение.
комментарий/решение
Задача №3. Запаздывание и затухание (16 баллов)
В этой задаче не следует учитывать конечность скорости распространения электромагнитного взаимодействия.
Часть 1. Магнитная. 1.1 Теоретическое введение
1.1.1. [0,75 балла] Покажите, что магнитное поле $B_z$ на оси диполя на больших расстояниях определяется формулой $$B_{z}=b p_{m}/z^{\beta},$$ где $z$ — координата, отсчитываемая вдоль оси диполя от его центра. Найдите значения параметров $b$ и $\beta$ в этой формуле.
1.1.2. [1 балл] Пусть виток с током (магнитный диполь) с магнитным моментом $p_m$ находится в неоднородном осесимметричном поле, индукция которого на оси $z$ зависит от координаты $z$ по закону $B_z (z)$. Ось диполя совпадает с осью симметрии поля. Покажите, что сила, действующая на диполь со стороны магнитного поля, определяется формулой $$F_{z}=-p_{m}\frac{sB_{z}}{dz}.$$ 1.2 Колебания магнита Цилиндрический магнит массы $m$, имеющий магнитный момент $p_m$, прикреплен к пружине жесткостью $k$ и способен совершать колебания вдоль горизонтальной оси, направленной вдоль магнитного момента.
1.2.1. [0,25 балла] Найдите частоту собственных колебаний магнита $\omega_0$ в отсутствие всех внешних полей. На расстоянии $z$ от положения равновесия магнита закрепляют небольшой металлический диск так, что его ось совпадает с осью магнита. Радиус диска $R$, его толщина $h$ $(h\ll R\ll z)$, удельное электрическое сопротивление материала диска равно $\rho$, магнитную проницаемость считайте равной $\mu=1$. Магнит выводят из положения равновесия и он начинает совершать малые колебания, описываемые некоторой функцией $x(t)$, причем $x\ll z$.
1.2.2. [2 балла] Найдите силу $F(x,v)$, действующую со стороны диска на магнит, как функцию его координаты x и скорости $v$. Запишите уравнение движения магнита.
1.2.3. [0,75 балла] Найдите относительное изменение частоты колебаний магнита $\Delta \omega/\omega_0$ из-за влияния диска.
1.2.4. [0,25 балла] Считая затухание колебаний слабыми, найдите характерное время затухания колебаний шарика.
1.2.5. [1,5 балла] Покажите, что потери механической энергии магнита равны количеству теплоты, выделившемуся в диске за то же время.
Математическая подсказка Уравнение затухающих колебаний $$x''+2\beta x'+\omega_0^2 x=0$$ имеет решение $$x(t)=A \exp(-t/\tau)\cos(\omega t+\varphi),$$ где $\omega=\sqrt{(\omega_0^2-\beta^2)}$ — частота затухающих колебаний, $\tau=1/\beta$ — характерное время затухания, параметры $A$, $\varphi$ определяются начальными условиями. При $x\ll 1$ можно приближённо считать, что $(1+x)^\alpha\thickapprox 1+\alpha x.$
Часть 2. Электрическая.
2.1 Теоретическое введение
2.1.1. [0,75 балла] Напряженность электрического поля, создаваемого диполем на его оси на расстоянии $z\gg l$, определяется формулой $$E=a \frac{p_{e}}{z^{\alpha}}.$$ Определите параметры $a$, $\alpha$ в этой формуле.
2.2 Колебания заряженного шарика.
Маленький шарик массы $m$, несущий электрический заряд $q$ прикреплен к непроводящей пружине жесткости $k$ и может совершать колебания вдоль горизонтальной оси $x$. На расстоянии $z$ от положения равновесия шарика закрепляют небольшой металлический идеально проводящий диск так, что его ось совпадает с осью $x$. Радиус диска $R$, его толщина $h$ $(h\ll R\ll z)$.
2.2.1. [0,75 балла] Найдите, насколько сместится положение равновесия шарика из-за влияния диска.
2.2.2. [0,75 балла] Найдите относительное изменение частоты колебаний шарика $\Delta \omega/\omega_0$ из-за влияния диска. Пусть теперь удельное электрическое сопротивление материала диска равно $\rho$.
2.2.3. [1,5 балла] Получите уравнение, описывающее изменение во времени индуцированного дипольного момента диска (т.е. связывающее дипольный момент диска $p$ и скорость его изменения во времени $dp/dt$).
2.2.4. [0,25 балла] Считая диск конденсатором, пластины которого соединены резистором, найдите характерное время такой $RC$-цепочки. Ответ выразите через удельное сопротивление $\rho$ материала диска. Далее будем считать, что характерное время, полученное в пункте 2.2.4, много меньше периода колебаний шарика.
2.2.5. [0,25 балла] Запишите следующее из этого условия соотношение между $\omega$ и $\rho$. Так как при идеальной проводимости диска колебания шарика будут незатухающими, при малом удельном сопротивлении материала диска затухание колебаний также должно быть малым, и такие колебания можно приближённо считать гармоническими.
2.2.6. [2 балла] Получите в этом приближении из уравнения, полученного в пункте 2.2.3, выражение дипольного момента диска $p$ через координату шарика $x$ и его скорость $v$.
2.2.7. [1,5 балла] Найдите выражение для силы, действующей на шарик со стороны диска. Запишите уравнение движения шарика. 2.2.8. [0,25 балла] Найдите характерное время затухания колебаний шарика. 2.2.9. [1,5 балла] Покажите, что потери механической энергии шарика равны количеству теплоты, выделившемуся в диске то же время.
комментарий/решение
В этой задаче не следует учитывать конечность скорости распространения электромагнитного взаимодействия.
Часть 1. Магнитная. 1.1 Теоретическое введение
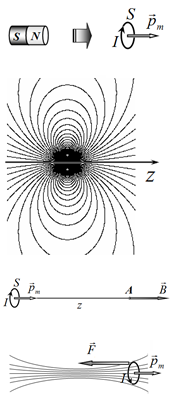
1.1.1. [0,75 балла] Покажите, что магнитное поле $B_z$ на оси диполя на больших расстояниях определяется формулой $$B_{z}=b p_{m}/z^{\beta},$$ где $z$ — координата, отсчитываемая вдоль оси диполя от его центра. Найдите значения параметров $b$ и $\beta$ в этой формуле.
1.1.2. [1 балл] Пусть виток с током (магнитный диполь) с магнитным моментом $p_m$ находится в неоднородном осесимметричном поле, индукция которого на оси $z$ зависит от координаты $z$ по закону $B_z (z)$. Ось диполя совпадает с осью симметрии поля. Покажите, что сила, действующая на диполь со стороны магнитного поля, определяется формулой $$F_{z}=-p_{m}\frac{sB_{z}}{dz}.$$ 1.2 Колебания магнита Цилиндрический магнит массы $m$, имеющий магнитный момент $p_m$, прикреплен к пружине жесткостью $k$ и способен совершать колебания вдоль горизонтальной оси, направленной вдоль магнитного момента.
1.2.1. [0,25 балла] Найдите частоту собственных колебаний магнита $\omega_0$ в отсутствие всех внешних полей. На расстоянии $z$ от положения равновесия магнита закрепляют небольшой металлический диск так, что его ось совпадает с осью магнита. Радиус диска $R$, его толщина $h$ $(h\ll R\ll z)$, удельное электрическое сопротивление материала диска равно $\rho$, магнитную проницаемость считайте равной $\mu=1$. Магнит выводят из положения равновесия и он начинает совершать малые колебания, описываемые некоторой функцией $x(t)$, причем $x\ll z$.
1.2.2. [2 балла] Найдите силу $F(x,v)$, действующую со стороны диска на магнит, как функцию его координаты x и скорости $v$. Запишите уравнение движения магнита.
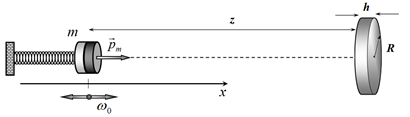
1.2.3. [0,75 балла] Найдите относительное изменение частоты колебаний магнита $\Delta \omega/\omega_0$ из-за влияния диска.
1.2.4. [0,25 балла] Считая затухание колебаний слабыми, найдите характерное время затухания колебаний шарика.
1.2.5. [1,5 балла] Покажите, что потери механической энергии магнита равны количеству теплоты, выделившемуся в диске за то же время.
Математическая подсказка Уравнение затухающих колебаний $$x''+2\beta x'+\omega_0^2 x=0$$ имеет решение $$x(t)=A \exp(-t/\tau)\cos(\omega t+\varphi),$$ где $\omega=\sqrt{(\omega_0^2-\beta^2)}$ — частота затухающих колебаний, $\tau=1/\beta$ — характерное время затухания, параметры $A$, $\varphi$ определяются начальными условиями. При $x\ll 1$ можно приближённо считать, что $(1+x)^\alpha\thickapprox 1+\alpha x.$
Часть 2. Электрическая.
2.1 Теоретическое введение
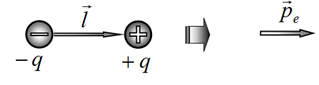
2.1.1. [0,75 балла] Напряженность электрического поля, создаваемого диполем на его оси на расстоянии $z\gg l$, определяется формулой $$E=a \frac{p_{e}}{z^{\alpha}}.$$ Определите параметры $a$, $\alpha$ в этой формуле.
2.2 Колебания заряженного шарика.
Маленький шарик массы $m$, несущий электрический заряд $q$ прикреплен к непроводящей пружине жесткости $k$ и может совершать колебания вдоль горизонтальной оси $x$. На расстоянии $z$ от положения равновесия шарика закрепляют небольшой металлический идеально проводящий диск так, что его ось совпадает с осью $x$. Радиус диска $R$, его толщина $h$ $(h\ll R\ll z)$.
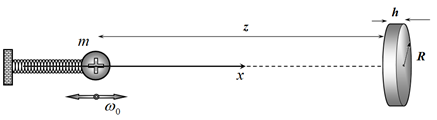
2.2.1. [0,75 балла] Найдите, насколько сместится положение равновесия шарика из-за влияния диска.
2.2.2. [0,75 балла] Найдите относительное изменение частоты колебаний шарика $\Delta \omega/\omega_0$ из-за влияния диска. Пусть теперь удельное электрическое сопротивление материала диска равно $\rho$.
2.2.3. [1,5 балла] Получите уравнение, описывающее изменение во времени индуцированного дипольного момента диска (т.е. связывающее дипольный момент диска $p$ и скорость его изменения во времени $dp/dt$).
2.2.4. [0,25 балла] Считая диск конденсатором, пластины которого соединены резистором, найдите характерное время такой $RC$-цепочки. Ответ выразите через удельное сопротивление $\rho$ материала диска. Далее будем считать, что характерное время, полученное в пункте 2.2.4, много меньше периода колебаний шарика.
2.2.5. [0,25 балла] Запишите следующее из этого условия соотношение между $\omega$ и $\rho$. Так как при идеальной проводимости диска колебания шарика будут незатухающими, при малом удельном сопротивлении материала диска затухание колебаний также должно быть малым, и такие колебания можно приближённо считать гармоническими.
2.2.6. [2 балла] Получите в этом приближении из уравнения, полученного в пункте 2.2.3, выражение дипольного момента диска $p$ через координату шарика $x$ и его скорость $v$.
2.2.7. [1,5 балла] Найдите выражение для силы, действующей на шарик со стороны диска. Запишите уравнение движения шарика. 2.2.8. [0,25 балла] Найдите характерное время затухания колебаний шарика. 2.2.9. [1,5 балла] Покажите, что потери механической энергии шарика равны количеству теплоты, выделившемуся в диске то же время.
комментарий/решение