Областная олимпиада по математике, 1999 год, 10 класс

Пусть $O$ — центр вневписанной окружности $\omega$ треугольника $ABC$ ($AB\neq AC$). Окружность $\omega$ касается стороны $BC$ в точке $K$, а с продолжениями сторон $AC$ и $AB$ в точках $M$ и $P$ соответственно. Определим точки: $T$ — точка пересечения прямых $AO$ и $PM$, $H$ — вторая точка пересечения окружности $\omega$ и прямой $AK$ Докажите, что точки $K$, $T$, $O$ и $H$ лежат на одной окружности.

Комментарий/решение

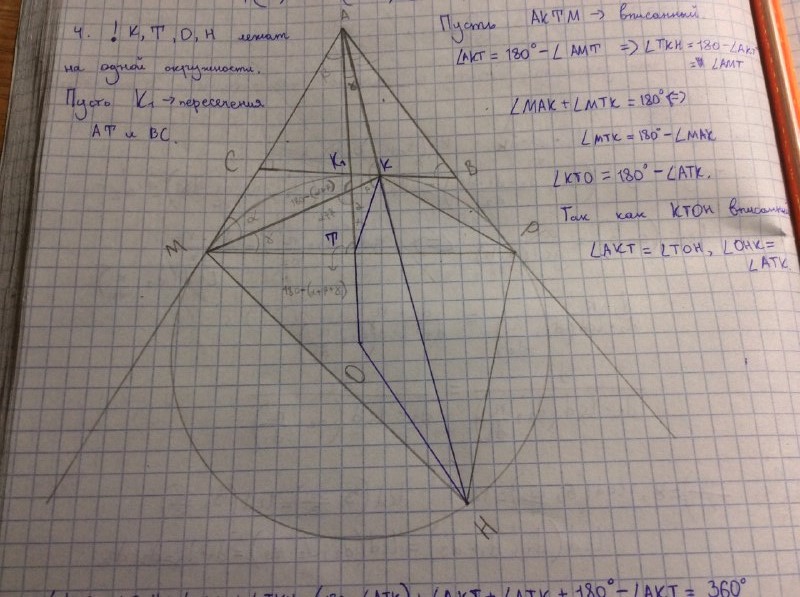
Пусть $\square AKTM$ вписанный (можно заметить через равенство углов). Тогда $$\angle AKT=180^\circ - \angle AMT$$ $$\Rightarrow \angle TKH = 180^\circ - \angle AKT = \angle AMT.$$

$$\angle MTK = 180^\circ - \angle MAK$$ . Так как $\square KTOH$ вписанный, $$\angle AKT = \angle TOH, \angle OHK =\angle ATK$$ . Тогда нам достаточно доказать, что сумма четырёхугольника $\square KTOH$ равен $360^\circ$

$$\angle KTO +\angle TOH + \angle OHK +\angle TKH = (180^\circ - \angle ATK) + \angle AKT +\angle ATK + (180^\circ - \angle AKT) = 360^\circ$$