Математикадан аудандық олимпиада, 2015-2016 оқу жылы, 8 сынып

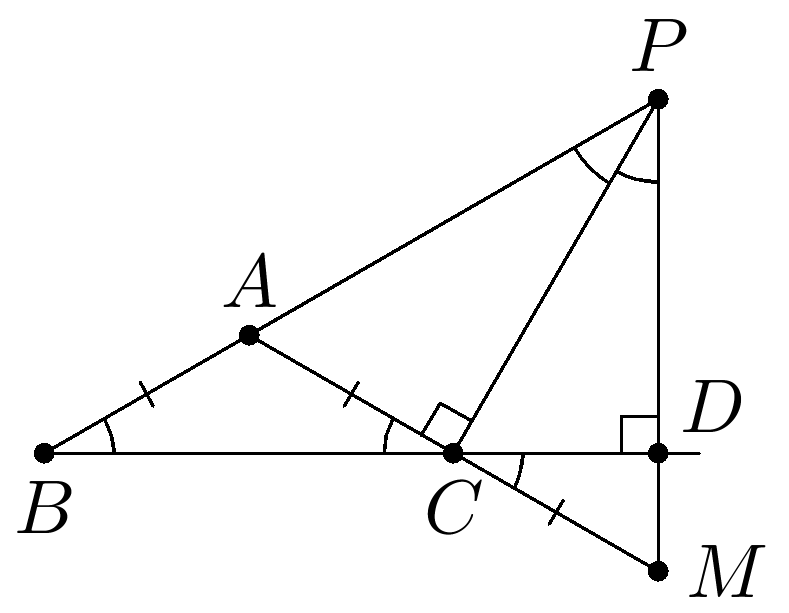
$ABC$ үшбұрышында $\angle A$ бұрышы доғал және $AB=AC$. $C$ — $AM$ кесіндісінің ортасы болатындай $M$ нүктесі алынған. $AM$ кесіндісіне жүргізілген орта перпендикуляр $AB$ түзуін $P$ нүктесінде қияды. $PM$ және $BC$ түзулері перпендикуляр екені белгілі. $APM$ — теңқабырғалы үшбұрыш екенін дәлелдеңіз.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.    
Решение. Известно, что сумма двух внутренних углов треугольника равна внешнему углу третьего. Пусть $\angle CBA=\angle BCA=\angle MCD= \alpha$, где $D$ — точка пересечения прямых $BC$ и $PM$. Тогда $\angle CMD= 90^\circ -\alpha$, откуда $\angle APC = \angle MPC=\alpha$, так как прямая $PC$ лежит на серединном перпендикуляре отрезка $AM$. Тогда из треугольника $BPC$ найдем $\angle PCD = 2 \alpha$, то есть $\angle PCM = 3 \alpha = 90^\circ$, откуда $\alpha=30^\circ$. Получается, что в равнобедренном треугольнике $APM$ $\angle APM = 2 \alpha = 60^\circ$.