Леонард Эйлер атындағы олимпиада,2013-2014 оқу жылы, қорытынды кезеңнің 1-ші туры

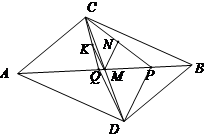
$C$ төбесіндегі бұрышы $100 ^\circ$ болатын $ABC$ үшбұрышының $AB$ қабырғасынан $AP=BC$ және $BQ=AC$ болатындай $P$ және $Q$ нүктелері алынған. $M$, $N$, $K$ нүктелері сәкесінше $AB$, $CP$, $CQ$ кесінділерінің орталары болсын. $NMK$ бұрышын анықтаңдар. ( М. Кунгожин, методкомиссия )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Ответ. $40 ^\circ$.
Решение. Достроим треугольник до параллелограмма $ACBD$. Тогда $M$ является серединой отрезка $CD$. Так как $AP = BC = AD$ и $BQ = AC = BD$, треугольники $APD$ и $BQD$ — равнобедренные. Поэтому $\angle QDP = \angle ADP+\angle BDQ - \angle ADB= (90^\circ - \angle DAB/2)+(90^\circ - \angle DBA/2) - 100^\circ = 80^\circ- \angle DAB+\angle DBA)/2 = 40 ^\circ$.
Осталось заметить, что $\angle QDP = \angle KMN$, так как $MK$ и $MN$ — средние линии треугольников $DQC$ и $DPC$ соответственно.