Олимпиада имени Леонарда Эйлера2010-2011 учебный год, IV тур дистанционного этапа
Петя раскладывает карточки с числами $1, 2, \dots, 9$ в клетки таблицы $3 \times 3$. Затем он отворачивается, а Витя меняет местами какие-то две карточки из клеток с общей стороной, и переворачивает все карточки лицом вниз. После этого Петя один раз показывает на одну или несколько карточек, а Витя сообщает сумму чисел на них. Сможет ли Петя действовать так, чтобы в результате гарантированно узнать, где какая карточка?
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Ответ. Сможет. Решение. Петя раскладывает карточки как нарисовано на рисунке:
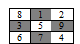
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.