Математикадан Эйлер олимпиадасы, 2010-2011 оқу жылы, Дистанциялық кезеңнің 4-ші туры
Петя $3 \times 3$ таблицасына $1$, $2$, $\ldots$, $9$ сандары жазылған карточкаларды қойып шығады. Ол теріс қарағаннан кейін, Витя, қабырғалары ортақ екі көршілес картаны орнымен ауыстырады да, барлық карталарды теріс қаратады. Содан кейін Петя бір рет бір немесе бірнеше картаға көрсетеді, ал Витя оған сол карталардың сандарының қосындысын айтады. Петя карталардың орналасуын кез келген жағдайда білетіндей стратегиясы бар ма?
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Ответ. Сможет. Решение. Петя раскладывает карточки как нарисовано на рисунке:
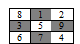
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.