Олимпиада имени Леонарда Эйлера2010-2011 учебный год, II тур дистанционного этапа
Внутри угла $AOB$, равного $120^\circ$, проведены лучи $OC$ и $OD$ так, что каждый из них является биссектрисой какого-то из углов, получившихся на чертеже. Найдите величину угла $AOC$. Укажите все возможные варианты.
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Ответ. $30^\circ$, $40^\circ$, $60^\circ$, $80^\circ$ или $90^\circ$. Решение. Если луч $OC$ — биссектриса угла $AOB$, то угол $AOC$ равен $60^\circ$ (независимо от того, является ли луч $OD$ биссектрисой угла $AOC$ или $BOC$). Если луч $OD$ — биссектриса угла $AOB$, то угол $AOC$ равен $30^\circ$ (если $OC$ — биссектриса угла $AOD$) или $90^\circ$ (если $OC$ — биссектриса угла $BOD$) Если луч $OC$ — биссектриса угла $AOD$, а луч $OD$ — биссектриса угла $BOC$ (рис. 3), то угол $AOC$ равен $60^\circ$. Аналогично, если луч $OD$ — биссектриса угла $AOC$, а луч $OC$ — биссектриса угла $BOD$ (рис. 4), то угол $AOC$ равен $80^\circ$.
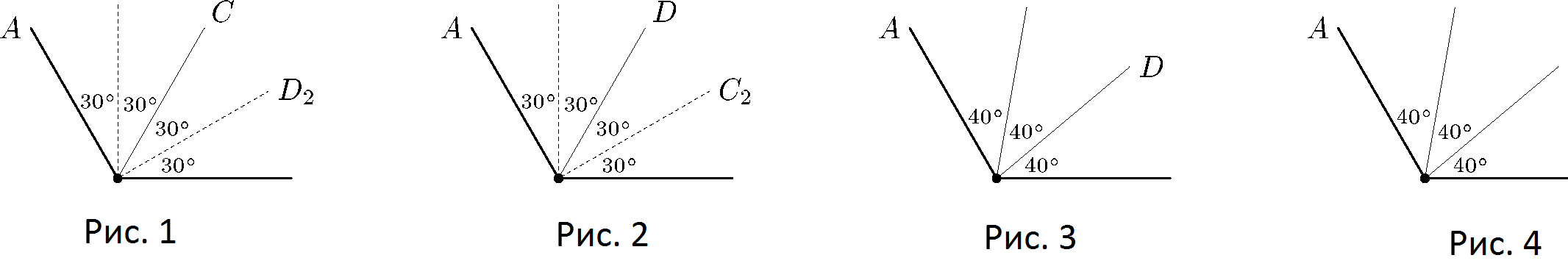
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.