Олимпиада имени Леонарда Эйлера2009-2010 учебный год, II тур дистанционного этапа

В треугольнике $ABC$ медиана $BM$ в два раза меньше стороны $AB$ и образует с ней угол в 40 градусов. Найдите угол $ABC$.

Комментарий/решение

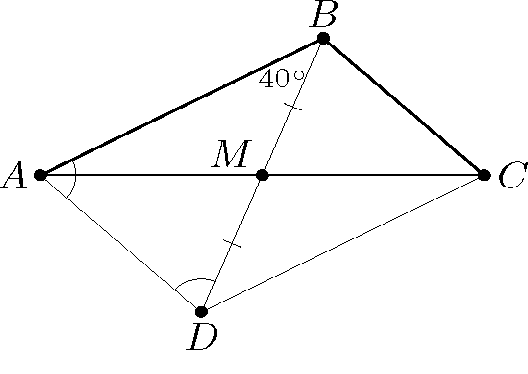
Комментарии от администратора Комментарии от администратора №1.     Ответ. $110^\circ$.
Решение. Продлим медиану $BM$ за точку $M$ на ее длину и получим точку $D$. Так как $AB = 2BM$, то $AB = BD$, то есть треугольник $ABD$ — равнобедренный. Следовательно, углы $BAD$ и $BDA$ равны по $(180^\circ-40^\circ):2 = 70^\circ$ каждый. $ABCD$ — параллелограмм, так как его диагонали точкой пересечения делятся пополам. Значит, угол $CBD$, как и $ADB$, равен $70^\circ$, а угол $ABC$, равный сумме $CBD$ и $ABD$, составляет $110^\circ$.