13-я Жаутыковская олимпиада (2017), теоретический тур
Есеп №1. (10,0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача 1А (3,0 балла) Испытывается новый скорострельный многоствольный пулемет, дающий $n=100$ выстрелов/с. Скорость полета пули составляет $u=1000$ м/с, а ее масса равна $m=10$ г. Мишенью служит вертикально подвешенный на канате ящик с песком, масса которого равна $M=1000$ кг. Считая, что пули застревают в ящике, определите максимальный угол отклонения ящика с песком от вертикали после начала стрельбы.
Задача 1В (4,0 балла) В космосе летает мыльный пузырь радиуса $R_1$. С помощью внешнего ионизатора мыльную пленку быстро заряжают некоторым положительным зарядом, после чего радиус пузыря через некоторое время перестаёт меняться и становится равным $R_2=2R_1$. Найдите электрический заряд $q$, который был сообщен мыльной пленке, если ее теплоемкость и теплопроводность ничтожно малы. Коэффициент поверхностного натяжения мыльной пленки не зависит от температуры и равен $\sigma$. Воздух считать идеальным двухатомным газом.
Задача 1С (3,0 балла) В точках $S_1$ и $S_2$ (смотрите выданный вам отдельный лист к этой задаче) находятся два одинаковых источника монохроматических когерентных волн с длиной волны $\lambda$. На листе длина волны соответствует размеру двух клеток. В точках $A_1$ и $A_2$ находятся приемники этих волн. Каждый источник излучает волну с интенсивностью $I_0$, изменением амплитуды волны при изменении расстояния до источника можно пренебречь. Построением на том же листе к этой задаче найдите, в каких точках выделенной овалом области следует поместить третий источник, чтобы он полностью подавил сигналы в точках $A_1$ и $A_2$ одновременно. Какова должна быть интенсивность волны от третьего источника? Все источники излучают волны с одинаковой фазой и поляризацией, перпендикулярной плоскости рисунка.
Внимание! Произведите все необходимые построения на выданном вам листе к этой задаче, впишите в него свои данные и сложите вместе с листами ответов $Writing sheets$, включив его в общую нумерацию. В противном случае, ваше решение оцениваться не будет!
комментарий/решение
Задача 1А (3,0 балла) Испытывается новый скорострельный многоствольный пулемет, дающий $n=100$ выстрелов/с. Скорость полета пули составляет $u=1000$ м/с, а ее масса равна $m=10$ г. Мишенью служит вертикально подвешенный на канате ящик с песком, масса которого равна $M=1000$ кг. Считая, что пули застревают в ящике, определите максимальный угол отклонения ящика с песком от вертикали после начала стрельбы.
Задача 1В (4,0 балла) В космосе летает мыльный пузырь радиуса $R_1$. С помощью внешнего ионизатора мыльную пленку быстро заряжают некоторым положительным зарядом, после чего радиус пузыря через некоторое время перестаёт меняться и становится равным $R_2=2R_1$. Найдите электрический заряд $q$, который был сообщен мыльной пленке, если ее теплоемкость и теплопроводность ничтожно малы. Коэффициент поверхностного натяжения мыльной пленки не зависит от температуры и равен $\sigma$. Воздух считать идеальным двухатомным газом.
Задача 1С (3,0 балла) В точках $S_1$ и $S_2$ (смотрите выданный вам отдельный лист к этой задаче) находятся два одинаковых источника монохроматических когерентных волн с длиной волны $\lambda$. На листе длина волны соответствует размеру двух клеток. В точках $A_1$ и $A_2$ находятся приемники этих волн. Каждый источник излучает волну с интенсивностью $I_0$, изменением амплитуды волны при изменении расстояния до источника можно пренебречь. Построением на том же листе к этой задаче найдите, в каких точках выделенной овалом области следует поместить третий источник, чтобы он полностью подавил сигналы в точках $A_1$ и $A_2$ одновременно. Какова должна быть интенсивность волны от третьего источника? Все источники излучают волны с одинаковой фазой и поляризацией, перпендикулярной плоскости рисунка.
Внимание! Произведите все необходимые построения на выданном вам листе к этой задаче, впишите в него свои данные и сложите вместе с листами ответов $Writing sheets$, включив его в общую нумерацию. В противном случае, ваше решение оцениваться не будет!
комментарий/решение
Есеп №2. (10,0 балла)
Фантастические путешествия по Вселенной
Разведывательный космический корабль развитой цивилизации бороздит просторы Вселенной. В этой задаче Вам предстоит рассмотреть несколько ситуаций этого межзвездного путешествия с физической точки зрения. Во всех численных расчетах считайте гравитационную постоянную известной и равной $G=6,672\times 10^{-11}$ м$^3$/(кг$\cdot$с$^2$).
1. Планеты диковинных форм (3,9 балла)
На некотором расстоянии от корабля капитан обнаружил первую планету, которая имела странную форму параллелепипеда с квадратным основанием $a$ и очень малой толщиной $h\ll a$. Капитан отдал приказ следовать на планету по курсу, показанному на рисунке. $$\includegraphics[scale=0.3]{Zhaut_2017_T_2_1_1}$$
После выключения двигателей обнаружилось, что ускорение свободного падения корабля $g$, сообщаемое ему планетой на расстояниях много больших $h$, пропорционально телесному углу $\Omega$, под которым планета видна с корабля, то есть: $$g=\alpha \Omega.$$ $$\includegraphics[scale=0.3]{Zhaut_2017_T_2_1_2}$$ Телесный угол $\Omega$ — это часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Границей телесного угла является некоторая коническая поверхность. Телесный угол измеряется отношением площади $S$ той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса $R$ сферы: $$\Omega=\frac{S}{R^2}.$$ Телесные углы измеряются отвлечёнными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы радиуса $R$ поверхность с площадью $R^2$. Полная сфера образует телесный угол, равный $4\pi$ стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы.
Высадившись на поверхность и взяв пробы грунта, ученые сообщили капитану, что планета состоит из однородного материала плотности $\rho_1=3000$ кг/м$^3$, а ускорение свободного падения вблизи геометрического центра поверхности практически постоянно и равно $g_1=9,81\times 10^{-2}$ м/с$^2$.
1.1 [0,7 балла] Найдите и рассчитайте толщину планеты $h$;
1.2 [0,5 балла] Найдите и рассчитайте коэффициент $\alpha$;
Покинув первую планету, капитан и его команда встретили еще более экзотическую планету, которая по форме представляла собой правильную пирамиду, с квадратным основанием со стороной $a=10 000$ км и высотой $\frac{a}{2}$.
1.3 [0,7 балла] Найдите и рассчитайте ускорение свободного падения $g_2$, измеренное на вершине однородной пирамидальной планеты, если ее плотность равна $\rho_2=4500$ кг/м$^3$.
Космический корабль покинул пирамидальную планету с ее вершины, стартовав со второй космической скоростью $\vartheta_1=3,45$ км/с. Следующей на пути встретилась планета, имеющая форму идеального куба со стороной $a$. Проведя измерения, капитан и его команда выяснили, что плотность кубической планеты равна $\rho_3=5000$ кг/м$^3$.
1.4 [2,0 балла] Найдите и рассчитайте вторую космическую скорость $\vartheta_2$ при старте корабля с одной из вершин кубической планеты.
2. Пылевое облако (6,1 балла) На пути корабля встречается очень большое массивное пылевое облако радиуса $R=1,5\times 10^7$ км c однородной плотностью $\rho_4=50$ кг/м$^3$. Скорость корабля на большом расстоянии от облака равна $\vartheta_{\infty}=100$ км/с, а прицельное расстояние до центра равно $b=1,5\times 10^8$ км. Двигатель корабля выключен. $$\includegraphics[scale=0.3]{Zhaut_2017_T_2_2}$$
2.1 [2,5 балла] Найдите и рассчитайте координату входа корабля в пылевое облако, характеризуемую углом $\theta$.
2.2 [2,0 балла] Найдите и рассчитайте минимальное расстояние $r_{\min}$, на котором корабль пролетит от центра облака. Сопротивлением частиц облака движению корабля можно пренебречь.
Определив таким образом, что избежать столкновения с облаком невозможно, капитан корабля включает двигатель, изменяя скорость $\vartheta_{\infty}$.
2.3 [1,0 балла] Найдите и рассчитайте минимальную скорость $\vartheta_{\infty,\min}$, при которой корабль минует облако.
Успешно миновав препятствие, капитан и его команда обнаружили, что частицы пылевого облака содержат ценные элементы.
2.4 [0,6 балла] Найдите минимальную работу $A$, которую необходимо совершить, чтобы постепенно доставить все пылевые частицы на очень удаленный перерабатывающий завод.
комментарий/решение
1. Планеты диковинных форм (3,9 балла)
На некотором расстоянии от корабля капитан обнаружил первую планету, которая имела странную форму параллелепипеда с квадратным основанием $a$ и очень малой толщиной $h\ll a$. Капитан отдал приказ следовать на планету по курсу, показанному на рисунке. $$\includegraphics[scale=0.3]{Zhaut_2017_T_2_1_1}$$
После выключения двигателей обнаружилось, что ускорение свободного падения корабля $g$, сообщаемое ему планетой на расстояниях много больших $h$, пропорционально телесному углу $\Omega$, под которым планета видна с корабля, то есть: $$g=\alpha \Omega.$$ $$\includegraphics[scale=0.3]{Zhaut_2017_T_2_1_2}$$ Телесный угол $\Omega$ — это часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Границей телесного угла является некоторая коническая поверхность. Телесный угол измеряется отношением площади $S$ той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса $R$ сферы: $$\Omega=\frac{S}{R^2}.$$ Телесные углы измеряются отвлечёнными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы радиуса $R$ поверхность с площадью $R^2$. Полная сфера образует телесный угол, равный $4\pi$ стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы.
Высадившись на поверхность и взяв пробы грунта, ученые сообщили капитану, что планета состоит из однородного материала плотности $\rho_1=3000$ кг/м$^3$, а ускорение свободного падения вблизи геометрического центра поверхности практически постоянно и равно $g_1=9,81\times 10^{-2}$ м/с$^2$.
1.1 [0,7 балла] Найдите и рассчитайте толщину планеты $h$;
1.2 [0,5 балла] Найдите и рассчитайте коэффициент $\alpha$;
Покинув первую планету, капитан и его команда встретили еще более экзотическую планету, которая по форме представляла собой правильную пирамиду, с квадратным основанием со стороной $a=10 000$ км и высотой $\frac{a}{2}$.
1.3 [0,7 балла] Найдите и рассчитайте ускорение свободного падения $g_2$, измеренное на вершине однородной пирамидальной планеты, если ее плотность равна $\rho_2=4500$ кг/м$^3$.
Космический корабль покинул пирамидальную планету с ее вершины, стартовав со второй космической скоростью $\vartheta_1=3,45$ км/с. Следующей на пути встретилась планета, имеющая форму идеального куба со стороной $a$. Проведя измерения, капитан и его команда выяснили, что плотность кубической планеты равна $\rho_3=5000$ кг/м$^3$.
1.4 [2,0 балла] Найдите и рассчитайте вторую космическую скорость $\vartheta_2$ при старте корабля с одной из вершин кубической планеты.
2. Пылевое облако (6,1 балла) На пути корабля встречается очень большое массивное пылевое облако радиуса $R=1,5\times 10^7$ км c однородной плотностью $\rho_4=50$ кг/м$^3$. Скорость корабля на большом расстоянии от облака равна $\vartheta_{\infty}=100$ км/с, а прицельное расстояние до центра равно $b=1,5\times 10^8$ км. Двигатель корабля выключен. $$\includegraphics[scale=0.3]{Zhaut_2017_T_2_2}$$
2.1 [2,5 балла] Найдите и рассчитайте координату входа корабля в пылевое облако, характеризуемую углом $\theta$.
2.2 [2,0 балла] Найдите и рассчитайте минимальное расстояние $r_{\min}$, на котором корабль пролетит от центра облака. Сопротивлением частиц облака движению корабля можно пренебречь.
Определив таким образом, что избежать столкновения с облаком невозможно, капитан корабля включает двигатель, изменяя скорость $\vartheta_{\infty}$.
2.3 [1,0 балла] Найдите и рассчитайте минимальную скорость $\vartheta_{\infty,\min}$, при которой корабль минует облако.
Успешно миновав препятствие, капитан и его команда обнаружили, что частицы пылевого облака содержат ценные элементы.
2.4 [0,6 балла] Найдите минимальную работу $A$, которую необходимо совершить, чтобы постепенно доставить все пылевые частицы на очень удаленный перерабатывающий завод.
комментарий/решение
Есеп №3. (10,0 балла)
Сопротивление призмы
1. Математическое введение (3,0 балла) По определению считается, что члены числовой последовательности $x_0,x_1,x_2,...$ подчиняются рекуррентному соотношению, если каждый последующий из них выражается через предыдущие. Например, для известной вам геометрической прогрессии $$x_{k}=\lambda x_{k-1},\quad (1)$$ где $k=1,2,3,...,\lambda$, $\lambda$ — некоторое фиксированное число, а нулевой член последовательности имеет некоторое значение $A$, то есть $x_0=A$.
1.1 [0,2 балла] Получите формулу для произвольного члена последовательности $x_{k}$ в явном виде, т.е. выразите его через номер $k$, начальное значение $A$ и $\lambda$.
Теперь рассмотрим число $\lambda=2+\sqrt{3}$. При возведении в целую натуральную степень $k$, его можно представить в виде $$\lambda^{k}=p_{k}+q_{k}\sqrt{3},\quad (2)$$ где $p_{k}$, $q_{k}$ — некоторые целые числа.
1.2 [0,4 балла] Запишите рекуррентные соотношения, выражающие значения $p_{k}$, $q_{k}$ через предыдущие значения $p_{k-1}$, $q_{k-1}$. Запишите также обратные соотношения, выражающие $p_{k-1}$, $q_{k-1}$ через $p_{k}$, $q_{k}$.
1.3 [0,7 балла] Рассчитайте численные значения коэффициентов $p_{k}$, $q_{k}$ для $k=1,2,3,4,5$.
1.4 [0,2 балла] Выразите число $\lambda^{-k}=(2+\sqrt3)^{-k}$ через найденные величины $p_{k}$, $q_{k}$.
Пусть члены некоторой числовой последовательности подчиняются рекуррентному соотношению $$x_{k+1}=4x_{k}-x_{k-1},\hspace{5px} k=1,...,N-1,\eqno(3)$$ причем известно, что $N$ — некоторое целое число, а $x_0=A$ и $x_{N}=B$, $A$, $B$ — произвольные числа.
1.5 [1,0 балла] Получите формулу для произвольного члена $x_{k}$ последовательности $(3)$ в явном виде, т.е. выразите его через номер $k$ и величины $A$, $B$, $N$.
1.6 [0,5 балла] Выразите произвольный член последовательности $x_{k}$ через величины $p_{k}$, $q_{k}$, найденные в пп.1.2-1.3.
Подсказка. Решение рекуррентного соотношения $(3)$ нужно искать в виде $x_{k}=C\lambda^{k}$, где $C$ — некоторая константа. Найдите, при каких значениях $\lambda$ это возможно и постройте общее решение, удовлетворяющее заданным условиям.
2. Проволочный каркас в форме призмы (7,0 балла)
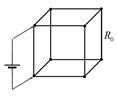
Широко известны задачи, в которых требуется найти электрическое сопротивление простейших проволочных каркасов. Пример одного из таких каркасов в форме куба показан на рисунке внизу. Пусть электрическое сопротивление каждого ребра равно $R_0$.
2.1 [0,8 балла] Найдите сопротивление куба при подключении источника к вершинам одного ребра, как показано на рисунке справа.
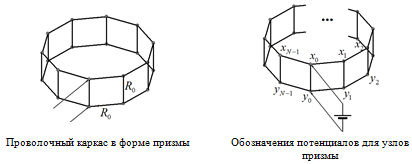
Давайте рассмотрим более общий случай проволочного каркаса в форме правильной призмы с произвольным числом боковых граней $N$ и определим его электрическое сопротивление при подключении источника к вершинам одного из боковых ребер, как показано на рисунке внизу. Сопротивление каждого ребра каркаса равно $R_0$.
Для удобства пронумеруем вершины призмы и обозначим их электрические потенциалы: на верхней грани $x_{k}$, а на нижней грани $y_{k}$, как показано на рисунке внизу. Источник постоянного напряжения подключен к вершинам нулевого ребра. Будем считать, что источник задает потенциалы вершин ребра равными $x_0=+\varphi_0$ и $y_0=-\varphi_0$ соответственно.
2.2 [0,2 балла] Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $y_{k}$. Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $x_{N-k}$.
Рассмотрим произвольное боковое ребро призмы, кроме нулевого $k=0$ и последнего $k=N-1$. Соответствующая электрическая схема показана на рисунке ниже.
2.3 [1,0 балла] Запишите соотношение, связывающие значения потенциала $x_{k}$ со значениями потенциалов в соседних вершинах для $k=1,2,...,N-2$.
2.4 [0,2 балла] Запишите граничные условия в точках $k=0$ и $k=N-1$, позволяющие определить значения потенциалов $x_{k}$ однозначно.
2.5 [0,2 балла] Найдите явные выражения для потенциалов $x_{k}$ и $y_{k}$ для всех значений $k=0,1,2,...,N-1$.
2.6 [0,4 балла] Выразите значение силы тока, протекающего через источник, через величины $\varphi_0$, $R_0$, $N$. Используйте найденные в Математическом введении числа $p_{k}$, $q_{k}$.
2.7 [0,2 балла] Получите явную формулу для сопротивления проволочного каркаса $R_{N}$, выразив его через величины $R_0$, $p_{N}$, $q_{N}$.
2.8 [1,0 балла] Рассчитайте точные значения сопротивлений каркаса для $N=1,2,3,4,5$.
2.9 [0,5 балла] Нарисуйте эквивалентные электрические схемы для «экзотических» призм с $N=1$ и $N=2$.
2.10 [1,0 балла] Найдите значения сопротивления $R_{\infty}$ каркаса при $N\to \infty$.
2.11 [1,5 балла] Найдите минимальное значение $N$, при котором сопротивление призмы отличается от $R_{\infty}$ не более чем на $2\%$.
комментарий/решение
1. Математическое введение (3,0 балла) По определению считается, что члены числовой последовательности $x_0,x_1,x_2,...$ подчиняются рекуррентному соотношению, если каждый последующий из них выражается через предыдущие. Например, для известной вам геометрической прогрессии $$x_{k}=\lambda x_{k-1},\quad (1)$$ где $k=1,2,3,...,\lambda$, $\lambda$ — некоторое фиксированное число, а нулевой член последовательности имеет некоторое значение $A$, то есть $x_0=A$.
1.1 [0,2 балла] Получите формулу для произвольного члена последовательности $x_{k}$ в явном виде, т.е. выразите его через номер $k$, начальное значение $A$ и $\lambda$.
Теперь рассмотрим число $\lambda=2+\sqrt{3}$. При возведении в целую натуральную степень $k$, его можно представить в виде $$\lambda^{k}=p_{k}+q_{k}\sqrt{3},\quad (2)$$ где $p_{k}$, $q_{k}$ — некоторые целые числа.
1.2 [0,4 балла] Запишите рекуррентные соотношения, выражающие значения $p_{k}$, $q_{k}$ через предыдущие значения $p_{k-1}$, $q_{k-1}$. Запишите также обратные соотношения, выражающие $p_{k-1}$, $q_{k-1}$ через $p_{k}$, $q_{k}$.
1.3 [0,7 балла] Рассчитайте численные значения коэффициентов $p_{k}$, $q_{k}$ для $k=1,2,3,4,5$.
1.4 [0,2 балла] Выразите число $\lambda^{-k}=(2+\sqrt3)^{-k}$ через найденные величины $p_{k}$, $q_{k}$.
Пусть члены некоторой числовой последовательности подчиняются рекуррентному соотношению $$x_{k+1}=4x_{k}-x_{k-1},\hspace{5px} k=1,...,N-1,\eqno(3)$$ причем известно, что $N$ — некоторое целое число, а $x_0=A$ и $x_{N}=B$, $A$, $B$ — произвольные числа.
1.5 [1,0 балла] Получите формулу для произвольного члена $x_{k}$ последовательности $(3)$ в явном виде, т.е. выразите его через номер $k$ и величины $A$, $B$, $N$.
1.6 [0,5 балла] Выразите произвольный член последовательности $x_{k}$ через величины $p_{k}$, $q_{k}$, найденные в пп.1.2-1.3.
Подсказка. Решение рекуррентного соотношения $(3)$ нужно искать в виде $x_{k}=C\lambda^{k}$, где $C$ — некоторая константа. Найдите, при каких значениях $\lambda$ это возможно и постройте общее решение, удовлетворяющее заданным условиям.
2. Проволочный каркас в форме призмы (7,0 балла)
Широко известны задачи, в которых требуется найти электрическое сопротивление простейших проволочных каркасов. Пример одного из таких каркасов в форме куба показан на рисунке внизу. Пусть электрическое сопротивление каждого ребра равно $R_0$.
2.1 [0,8 балла] Найдите сопротивление куба при подключении источника к вершинам одного ребра, как показано на рисунке справа.
Давайте рассмотрим более общий случай проволочного каркаса в форме правильной призмы с произвольным числом боковых граней $N$ и определим его электрическое сопротивление при подключении источника к вершинам одного из боковых ребер, как показано на рисунке внизу. Сопротивление каждого ребра каркаса равно $R_0$.
Для удобства пронумеруем вершины призмы и обозначим их электрические потенциалы: на верхней грани $x_{k}$, а на нижней грани $y_{k}$, как показано на рисунке внизу. Источник постоянного напряжения подключен к вершинам нулевого ребра. Будем считать, что источник задает потенциалы вершин ребра равными $x_0=+\varphi_0$ и $y_0=-\varphi_0$ соответственно.
2.2 [0,2 балла] Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $y_{k}$. Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $x_{N-k}$.
Рассмотрим произвольное боковое ребро призмы, кроме нулевого $k=0$ и последнего $k=N-1$. Соответствующая электрическая схема показана на рисунке ниже.
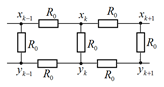
2.3 [1,0 балла] Запишите соотношение, связывающие значения потенциала $x_{k}$ со значениями потенциалов в соседних вершинах для $k=1,2,...,N-2$.
2.4 [0,2 балла] Запишите граничные условия в точках $k=0$ и $k=N-1$, позволяющие определить значения потенциалов $x_{k}$ однозначно.
2.5 [0,2 балла] Найдите явные выражения для потенциалов $x_{k}$ и $y_{k}$ для всех значений $k=0,1,2,...,N-1$.
2.6 [0,4 балла] Выразите значение силы тока, протекающего через источник, через величины $\varphi_0$, $R_0$, $N$. Используйте найденные в Математическом введении числа $p_{k}$, $q_{k}$.
2.7 [0,2 балла] Получите явную формулу для сопротивления проволочного каркаса $R_{N}$, выразив его через величины $R_0$, $p_{N}$, $q_{N}$.
2.8 [1,0 балла] Рассчитайте точные значения сопротивлений каркаса для $N=1,2,3,4,5$.
2.9 [0,5 балла] Нарисуйте эквивалентные электрические схемы для «экзотических» призм с $N=1$ и $N=2$.
2.10 [1,0 балла] Найдите значения сопротивления $R_{\infty}$ каркаса при $N\to \infty$.
2.11 [1,5 балла] Найдите минимальное значение $N$, при котором сопротивление призмы отличается от $R_{\infty}$ не более чем на $2\%$.
комментарий/решение