13-я Жаутыковская олимпиада (2017), теоретический тур

(10,0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача 1А (3,0 балла) Испытывается новый скорострельный многоствольный пулемет, дающий $n=100$ выстрелов/с. Скорость полета пули составляет $u=1000$ м/с, а ее масса равна $m=10$ г. Мишенью служит вертикально подвешенный на канате ящик с песком, масса которого равна $M=1000$ кг. Считая, что пули застревают в ящике, определите максимальный угол отклонения ящика с песком от вертикали после начала стрельбы.
Задача 1В (4,0 балла) В космосе летает мыльный пузырь радиуса $R_1$. С помощью внешнего ионизатора мыльную пленку быстро заряжают некоторым положительным зарядом, после чего радиус пузыря через некоторое время перестаёт меняться и становится равным $R_2=2R_1$. Найдите электрический заряд $q$, который был сообщен мыльной пленке, если ее теплоемкость и теплопроводность ничтожно малы. Коэффициент поверхностного натяжения мыльной пленки не зависит от температуры и равен $\sigma$. Воздух считать идеальным двухатомным газом.
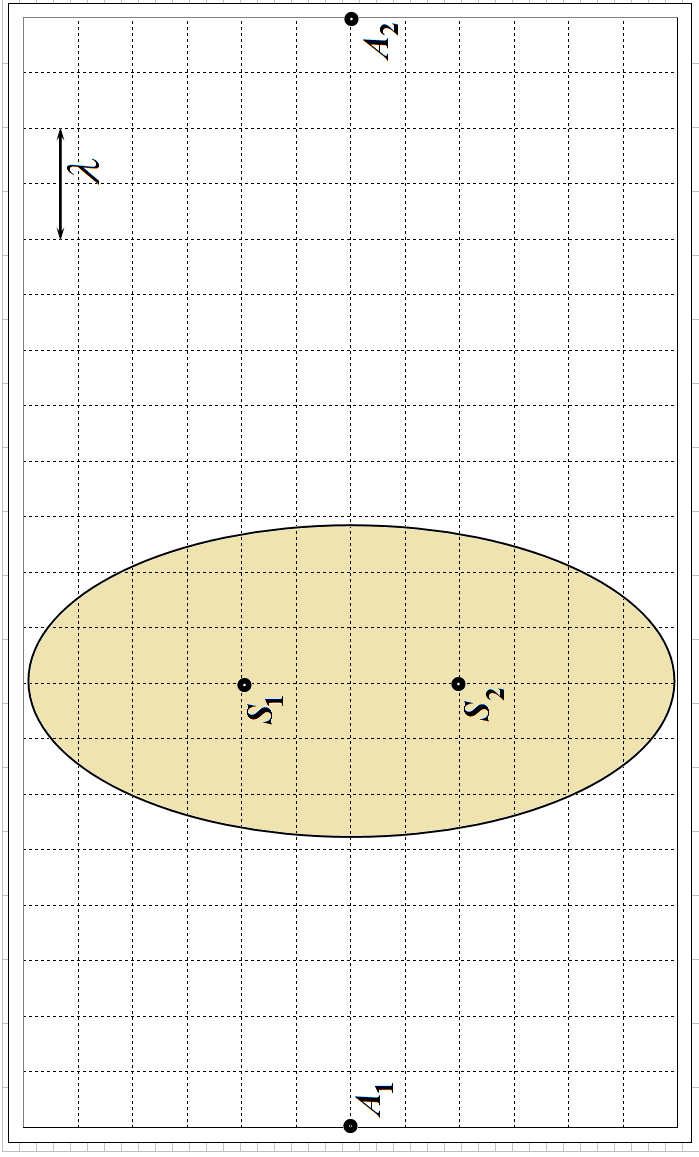
Задача 1С (3,0 балла) В точках $S_1$ и $S_2$ (смотрите выданный вам отдельный лист к этой задаче) находятся два одинаковых источника монохроматических когерентных волн с длиной волны $\lambda$. На листе длина волны соответствует размеру двух клеток. В точках $A_1$ и $A_2$ находятся приемники этих волн. Каждый источник излучает волну с интенсивностью $I_0$, изменением амплитуды волны при изменении расстояния до источника можно пренебречь. Построением на том же листе к этой задаче найдите, в каких точках выделенной овалом области следует поместить третий источник, чтобы он полностью подавил сигналы в точках $A_1$ и $A_2$ одновременно. Какова должна быть интенсивность волны от третьего источника? Все источники излучают волны с одинаковой фазой и поляризацией, перпендикулярной плоскости рисунка.

Внимание! Произведите все необходимые построения на выданном вам листе к этой задаче, впишите в него свои данные и сложите вместе с листами ответов $Writing sheets$, включив его в общую нумерацию. В противном случае, ваше решение оцениваться не будет!