9-я Жаутыковская олимпиада (2013), теоретический тур
Задача №1. (10 баллов)
Эта задача состоит из трех частей, не связанных друг с другом. Задача 1.А Блок (5.0 балла) На круглый блок радиуса $R$ положили канат длиной $L$ и массы $m$, который начал соскальзывать с блока без трения. В момент, когда разность высот свисающих с блока концов каната равна половине длины каната, найти:
1. ускорение каната;
2. натяжение каната в верхней точке;
3. точку каната, в которой сила натяжения максимальна (достаточно найти угол между радиусом в эту точку и вертикалью).
Задача 1.В. Запарь (2.0 балла) В физической лаборатории термометр показывал $20^{\circ}$ C, а барометр — $1$ атм. Лаборант Запарь достал из шкафа прочный сосуд, налил в него немного воды и герметично закрыл крышкой. Затем Запарь медленно нагрел сосуд до $200^{\circ}$ C. При этой температуре давление в сосуде составило $2,88$ атм. Определите температуру, при которой вся вода испарилась.
Задача 1.С. Пирамида (3.0 балла) Правильная треугольная пирамида $ABCD$ изготовлена из прозрачного материала с показателем преломления $n=1,6$. Все углы при вершине пирамиды $A$ — прямые. В основании пирамиды лежит правильный треугольник $BCD$, длины сторон которого равны $a=2$ мм. Эту пирамиду также можно представить, как «угол, отрезанный от куба». Пирамида однородно освещается так, что свет падает вдоль ее высоты, перпендикулярно плоскости основания.
1. Нарисуйте, область на основании пирамиды, освещенную светом, преломленным гранью $ABC$;
2. Параллельно основанию пирамиды на расстоянии $L=10$ см от него расположен экран. Нарисуйте области освещенные светом, преломленным пирамидой, на этом экране. Укажите положение и размеры этих областей.
комментарий/решение
Эта задача состоит из трех частей, не связанных друг с другом. Задача 1.А Блок (5.0 балла) На круглый блок радиуса $R$ положили канат длиной $L$ и массы $m$, который начал соскальзывать с блока без трения. В момент, когда разность высот свисающих с блока концов каната равна половине длины каната, найти:
1. ускорение каната;
2. натяжение каната в верхней точке;
3. точку каната, в которой сила натяжения максимальна (достаточно найти угол между радиусом в эту точку и вертикалью).
Задача 1.В. Запарь (2.0 балла) В физической лаборатории термометр показывал $20^{\circ}$ C, а барометр — $1$ атм. Лаборант Запарь достал из шкафа прочный сосуд, налил в него немного воды и герметично закрыл крышкой. Затем Запарь медленно нагрел сосуд до $200^{\circ}$ C. При этой температуре давление в сосуде составило $2,88$ атм. Определите температуру, при которой вся вода испарилась.
Задача 1.С. Пирамида (3.0 балла) Правильная треугольная пирамида $ABCD$ изготовлена из прозрачного материала с показателем преломления $n=1,6$. Все углы при вершине пирамиды $A$ — прямые. В основании пирамиды лежит правильный треугольник $BCD$, длины сторон которого равны $a=2$ мм. Эту пирамиду также можно представить, как «угол, отрезанный от куба». Пирамида однородно освещается так, что свет падает вдоль ее высоты, перпендикулярно плоскости основания.
1. Нарисуйте, область на основании пирамиды, освещенную светом, преломленным гранью $ABC$;
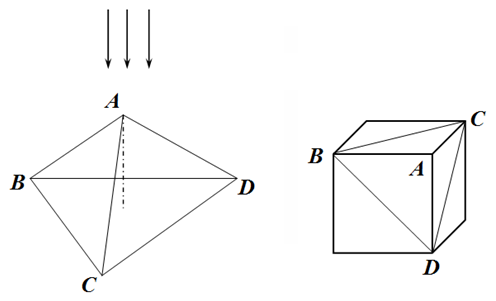
2. Параллельно основанию пирамиды на расстоянии $L=10$ см от него расположен экран. Нарисуйте области освещенные светом, преломленным пирамидой, на этом экране. Укажите положение и размеры этих областей.
комментарий/решение
Задача №2. Квадратная рамка (10 баллов)
1. [0.2 балла] В вашем решении перерисуйте схематически этот рисунок и укажите, какой из полюсов магнита является северным $N$, а какой южным $S$.
Часть А. Пусть рамка изготовлена из проводящего материала, имеет сопротивление $R=10^{-2}$ Ом и пренебрежимо малую индуктивность. В момент времени $t=0$ к рамке прикладывается постоянная сила $F=10^{-4}$ Н, с помощью которой она вытягивается из магнитного поля.
2. [1.2 балла] Найдите аналитическую зависимость скорости рамки $v(t)$ от времени $t$, считая, что рамка все время остается между полюсами магнита. Запишите ответ через $B$, $a$, $m$, $R$ и $t$.
3. [0.8 балла] Запишите точное уравнение для определения времени $t_0$ нахождения рамки между полюсами магнита. Запишите ответ через $B$, $a$, $m$, $R$ и $t_0$. Приближенно вычислите время $t_0$.
4. [1.2 балла] Постройте график зависимости скорости рамки $v(t)$ от времени $t$ за интервал от $0$ до $12$ с.
5. [1.2 балла] Постройте график зависимости тока в рамке $I(t)$ от времени $t$ за интервал от $0$ до $12$ с.
Часть B. Пусть рамка изготовлена из сверхпроводящего материала, имеет индуктивность $L=10^{-1}$ Гн, ту же массу и размеры. В момент времени $t=0$ к рамке прикладывается постоянная сила $F$, с помощью которой она вытягивается из магнитного поля.
6. [1.8 балла] Найдите минимальную силу $F_{\min}$, при которой рамку удастся вытянуть из магнита. Выразите ваш ответ через $B$, $a$, $L$ и рассчитайте численное значение.
7. [0.6 балла] В условиях предыдущего пункта найдите минимальное время $t_0$ до максимального выдвижения рамки из магнита. Выразите ваш ответ через $m$, $B$, $a$, $L$ и рассчитайте численное значение.
8. [1.0 балла] Постройте график зависимости тока в рамке от времени за интервал времени от $0$ до $4t_0$.
Часть C. Квадратная рамка со стороной $a$ изготовлена из проводящего материала, имеет индуктивность $L$, сопротивление $R$ и массу $m$. В момент времени $t=0$ рамке сообщают начальную скорость $v_0$, направленную так же, как и сила на рисунке сверху. Известно, что в момент, когда рамка практически покидает магнит, ее скорость обращается в ноль.
9. [2.0 балла] Найдите аналитическое выражение для силы тока $I_0$ в рамке в момент времени, когда ее скорость обращается в ноль. Запишите ответ через $B$, $a$, $m$, $L$, $R$ и $v_0$.
комментарий/решение
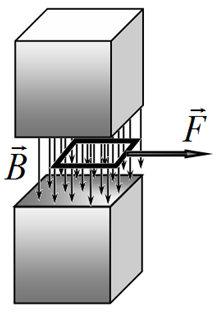
1. [0.2 балла] В вашем решении перерисуйте схематически этот рисунок и укажите, какой из полюсов магнита является северным $N$, а какой южным $S$.
Часть А. Пусть рамка изготовлена из проводящего материала, имеет сопротивление $R=10^{-2}$ Ом и пренебрежимо малую индуктивность. В момент времени $t=0$ к рамке прикладывается постоянная сила $F=10^{-4}$ Н, с помощью которой она вытягивается из магнитного поля.
2. [1.2 балла] Найдите аналитическую зависимость скорости рамки $v(t)$ от времени $t$, считая, что рамка все время остается между полюсами магнита. Запишите ответ через $B$, $a$, $m$, $R$ и $t$.
3. [0.8 балла] Запишите точное уравнение для определения времени $t_0$ нахождения рамки между полюсами магнита. Запишите ответ через $B$, $a$, $m$, $R$ и $t_0$. Приближенно вычислите время $t_0$.
4. [1.2 балла] Постройте график зависимости скорости рамки $v(t)$ от времени $t$ за интервал от $0$ до $12$ с.
5. [1.2 балла] Постройте график зависимости тока в рамке $I(t)$ от времени $t$ за интервал от $0$ до $12$ с.
Часть B. Пусть рамка изготовлена из сверхпроводящего материала, имеет индуктивность $L=10^{-1}$ Гн, ту же массу и размеры. В момент времени $t=0$ к рамке прикладывается постоянная сила $F$, с помощью которой она вытягивается из магнитного поля.
6. [1.8 балла] Найдите минимальную силу $F_{\min}$, при которой рамку удастся вытянуть из магнита. Выразите ваш ответ через $B$, $a$, $L$ и рассчитайте численное значение.
7. [0.6 балла] В условиях предыдущего пункта найдите минимальное время $t_0$ до максимального выдвижения рамки из магнита. Выразите ваш ответ через $m$, $B$, $a$, $L$ и рассчитайте численное значение.
8. [1.0 балла] Постройте график зависимости тока в рамке от времени за интервал времени от $0$ до $4t_0$.
Часть C. Квадратная рамка со стороной $a$ изготовлена из проводящего материала, имеет индуктивность $L$, сопротивление $R$ и массу $m$. В момент времени $t=0$ рамке сообщают начальную скорость $v_0$, направленную так же, как и сила на рисунке сверху. Известно, что в момент, когда рамка практически покидает магнит, ее скорость обращается в ноль.
9. [2.0 балла] Найдите аналитическое выражение для силы тока $I_0$ в рамке в момент времени, когда ее скорость обращается в ноль. Запишите ответ через $B$, $a$, $m$, $L$, $R$ и $v_0$.
комментарий/решение
Задача №3. Модель атома водорода по Бору (10 баллов)
Рассмотрим атом водорода, который состоит из протона, массу которого можно считать практически бесконечной, и электрона массой $m_{e}=9,11\times 10^{-31}$ кг. При этом протон имеет положительный заряд $e=1,61\times 10^{-19}$ Кл, а электрон — отрицательный заряд $-e$, так что в целом атом нейтрален.
1. [2.0 балла] Известно, что большинство атомов стабильно и могут существовать продолжительное время. Это значит, что электрон не может находиться в состоянии покоя, иначе под действием силы притяжения он неминуемо упал бы на протон. Пусть расстояние между электроном и протоном равно $r_0=5\times 10^{-11}$ м. Считая применимыми законы классической физики, найдите время падения $t_1$ первоначально покоящегося электрона на протон. Значит, для стабильности атома электрон должен двигаться вокруг протона так же, как планеты вращаются вокруг Солнца. Пусть орбита электрона круговая и законы классической физики по-прежнему применимы.
2. [1.0 балла] Найдите скорость движения электрона $v$ в зависимости от радиуса орбиты $r$;
3. [0.5 балла] Найдите момент импульса движения электрона $L$ в зависимости от радиуса орбиты $r$; Датский физик Нильс Бор выдвинул постулат о том, что момент импульса электрона равен целому числу постоянных Планка $\hbar=1,05\times10^{-34}$ Дж$\cdot$с, то есть $L=n\hbar$, где $n=1,2,3...$ — главное квантовое число.
4. [0.5 балла] Найдите возможные радиусы орбит электрона $r_{n}$ в атоме водорода;
5. [0.5 балла] Рассчитайте численное значение минимального радиуса орбиты электрона $r_1$ в атоме водорода;
6. [1.0 балла] Найдите возможные значения полной энергии электрона $E_{n}$ в атоме водорода;
7. [0.5 балла] Рассчитайте численное значение минимального значения полной энергии электрона $E_1$ в атоме водорода. Согласно классической электродинамике, если электрон движется с ускорением, то он теряет свою энергию на электромагнитное излучение. При этом мощность излучения определяется выражением $$P=\frac{1}{6 \pi \epsilon_0}\cdot \frac{e^2a^2}{c^3},$$ где $a$ — ускорение электрона,$\epsilon_0=8,85\times 10^{-12}$ Ф/м — электрическая постоянная, $c=3\times 10^8$ м/c — скорость света в вакууме. Электромагнитное излучение привело бы к тому, что в модели Бора электрон падал бы на протон. В дальнейшем считайте, что траектория электрона практически круговая.
8. [1.5 балла] Считая, что в момент времени $t=0$ электрон находится на орбите радиусом $r_1$, найдите зависимость радиуса траектории от времени $t$.
9. [0.5 балла] Найдите и вычислите время падения электрона $\tau_1$ с орбиты радиусом $r_1$ на протон.
10. [2.0 балла] Сколько оборотов успевает сделать электрон вокруг протона за время падения $\tau_1$?
комментарий/решение
Рассмотрим атом водорода, который состоит из протона, массу которого можно считать практически бесконечной, и электрона массой $m_{e}=9,11\times 10^{-31}$ кг. При этом протон имеет положительный заряд $e=1,61\times 10^{-19}$ Кл, а электрон — отрицательный заряд $-e$, так что в целом атом нейтрален.
1. [2.0 балла] Известно, что большинство атомов стабильно и могут существовать продолжительное время. Это значит, что электрон не может находиться в состоянии покоя, иначе под действием силы притяжения он неминуемо упал бы на протон. Пусть расстояние между электроном и протоном равно $r_0=5\times 10^{-11}$ м. Считая применимыми законы классической физики, найдите время падения $t_1$ первоначально покоящегося электрона на протон. Значит, для стабильности атома электрон должен двигаться вокруг протона так же, как планеты вращаются вокруг Солнца. Пусть орбита электрона круговая и законы классической физики по-прежнему применимы.
2. [1.0 балла] Найдите скорость движения электрона $v$ в зависимости от радиуса орбиты $r$;
3. [0.5 балла] Найдите момент импульса движения электрона $L$ в зависимости от радиуса орбиты $r$; Датский физик Нильс Бор выдвинул постулат о том, что момент импульса электрона равен целому числу постоянных Планка $\hbar=1,05\times10^{-34}$ Дж$\cdot$с, то есть $L=n\hbar$, где $n=1,2,3...$ — главное квантовое число.
4. [0.5 балла] Найдите возможные радиусы орбит электрона $r_{n}$ в атоме водорода;
5. [0.5 балла] Рассчитайте численное значение минимального радиуса орбиты электрона $r_1$ в атоме водорода;
6. [1.0 балла] Найдите возможные значения полной энергии электрона $E_{n}$ в атоме водорода;
7. [0.5 балла] Рассчитайте численное значение минимального значения полной энергии электрона $E_1$ в атоме водорода. Согласно классической электродинамике, если электрон движется с ускорением, то он теряет свою энергию на электромагнитное излучение. При этом мощность излучения определяется выражением $$P=\frac{1}{6 \pi \epsilon_0}\cdot \frac{e^2a^2}{c^3},$$ где $a$ — ускорение электрона,$\epsilon_0=8,85\times 10^{-12}$ Ф/м — электрическая постоянная, $c=3\times 10^8$ м/c — скорость света в вакууме. Электромагнитное излучение привело бы к тому, что в модели Бора электрон падал бы на протон. В дальнейшем считайте, что траектория электрона практически круговая.
8. [1.5 балла] Считая, что в момент времени $t=0$ электрон находится на орбите радиусом $r_1$, найдите зависимость радиуса траектории от времени $t$.
9. [0.5 балла] Найдите и вычислите время падения электрона $\tau_1$ с орбиты радиусом $r_1$ на протон.
10. [2.0 балла] Сколько оборотов успевает сделать электрон вокруг протона за время падения $\tau_1$?
комментарий/решение