5-я Жаутыковская олимпиада (2009), теоретический тур
Задача №1. Эта задача состоит из четырех частей, не связанных друг с другом.
1А (2 балла).
1В (3 балла).
1C (2 балла).
1. Выразите неизвестное сопротивление $R_{x}$ через сопротивления $R_1$, $R_2$, $R_0$ при условии сбалансированности моста.
2. В реальных измерениях практически невозможно точно зафиксировать отсутствие тока через миллиамперметр, так как его чувствительность ограничена. Пусть минимальное значение силы тока, которое может зафиксировать миллиамперметр равно $i_0$ (то есть при $i1D (3 балла).
Солнечным утром на освещаемом солнцем сухом асфальте видны блестящие пятна, похожие на лужи воды. Их появление является простейшим миражом — реально в этих «лужах» мы видим отражение неба.
Цель данной задачи дать теоретическое описание этого явления.
Показатель преломления воздуха $n$ зависит от концентрации молекул $\gamma$ в соответствии с формулой $$n=1+\frac{\alpha \gamma}{2},\quad (1)$$
где $\alpha=2,3\cdot 10^{-29}$ м$^3$ — средняя поляризуемость молекул воздуха. Будем считать, что температура воздуха равна $t_0=20^{\circ}$ С, атмосферное давление $P_0=1,0\cdot 10^5$ Па. Благодаря солнечным лучам у поверхности асфальта образуется тонкий слой более нагретого воздуха, температура которого на $\Delta t=2,0^{\circ}$ С выше, чем температура более высоких слоев.
Водитель движется прямолинейно по горизонтальной дороге, причем его глаза находятся на высоте $h=1,2$ м над поверхностью асфальта. Оцените, на каком расстоянии от водителя он может увидеть ближайшую к нему лужу-мираж.
Постоянная Больцмана $k_{B}=1,38\cdot 10^{-23}$ Дж/К.
При решении данных задач вы можете использовать приближенные формулы справедливые при малых значениях $x$:
$$(1+x)^{\gamma} \thickapprox 1+\gamma x$$
$$\sin x\thickapprox x$$
$$\cos x\thickapprox 1-\frac{x^2}{2}$$
комментарий/решение
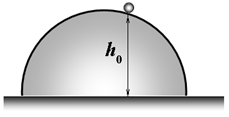
1А (2 балла).
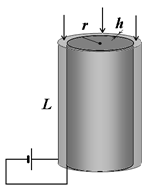
1В (3 балла).
1C (2 балла).
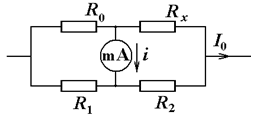
1. Выразите неизвестное сопротивление $R_{x}$ через сопротивления $R_1$, $R_2$, $R_0$ при условии сбалансированности моста.
2. В реальных измерениях практически невозможно точно зафиксировать отсутствие тока через миллиамперметр, так как его чувствительность ограничена. Пусть минимальное значение силы тока, которое может зафиксировать миллиамперметр равно $i_0$ (то есть при $i
комментарий/решение
Задача №2. Электромагнитные качели (10 баллов)
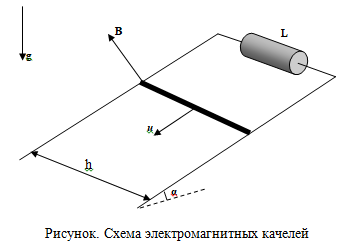
Два длинных проводящих стержня, соединённых вверху катушкой с индуктивностью $L$, образуют наклонную плоскость, составляющую угол $\alpha$ с горизонтом. Подвижный про-водник массой $m$ (см. рис.) способен скользить по стержням, всё время оставаясь перпендикулярным к ним и сохраняя с ними хороший электрический контакт. Коэффициент трения скольжения между проводником и стержнями равен $\mu$, расстояние между стержнями равно $g$, ускорение свободного падения равно $g$. Вся система помещена в перпендикулярное наклонной плоскости однородное магнитное поле с индукцией $B$. В данной задаче полностью пренебрегается омическим сопротивлением и индуктивностью стержней и проводника. Считая, что в начальный момент времени проводник покоится, а затем без толчка освобождается, дайте ответы на следующие вопросы.
комментарий/решение
Два длинных проводящих стержня, соединённых вверху катушкой с индуктивностью $L$, образуют наклонную плоскость, составляющую угол $\alpha$ с горизонтом. Подвижный про-водник массой $m$ (см. рис.) способен скользить по стержням, всё время оставаясь перпендикулярным к ним и сохраняя с ними хороший электрический контакт. Коэффициент трения скольжения между проводником и стержнями равен $\mu$, расстояние между стержнями равно $g$, ускорение свободного падения равно $g$. Вся система помещена в перпендикулярное наклонной плоскости однородное магнитное поле с индукцией $B$. В данной задаче полностью пренебрегается омическим сопротивлением и индуктивностью стержней и проводника. Считая, что в начальный момент времени проводник покоится, а затем без толчка освобождается, дайте ответы на следующие вопросы.
- Запишите неравенство, при выполнении которого проводник начнёт свое движение вниз после отпускания. Ответ выразите через $\alpha$, $\mu$; (1 балл)
- Считая, что условия вопроса $1$ выполнены и проводник начал движение вниз, найдите зависимость силы тока $I$ в катушке индуктивности от смещения $x$ проводника от начального положения. Ответ выразите через $h$, $B$, $L$, $x$; (2 балла)
- Найдите максимальную скорость проводника $u_{\max}$ в процессе его движения. Ответ выразите через $h$, $B$, $L$, $m$, $\alpha$, $g$, $\mu$; (1 балл)
- Найдите максимальную силу тока $I_{\max}$ в катушке индуктивности в процессе движения проводника. Ответ выразите через $h$, $B$, $m$, $\alpha$, $g$, $\mu$; (1 балл)
- Вычислите количество выделившейся из-за трения теплоты за очень большое время в случае малой силы трения. Ответ выразите через $h$, $B$, $L$, $m$, $\alpha$, $g$; (3 балла)
- Какова относительная ошибка ответа предыдущего пункта в случае $\mu=\frac{tg \alpha}{2009}$? (2 балла)
комментарий/решение
Задача №3. Тепловое излучение (10 баллов)
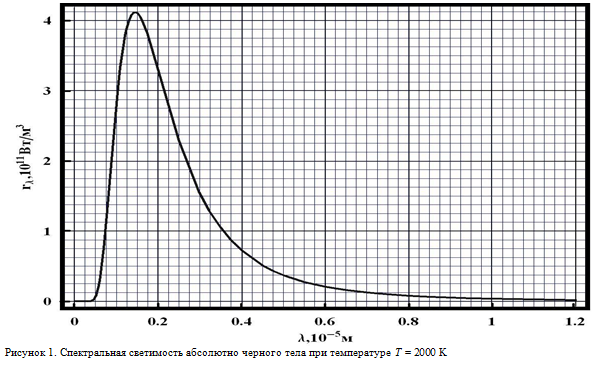
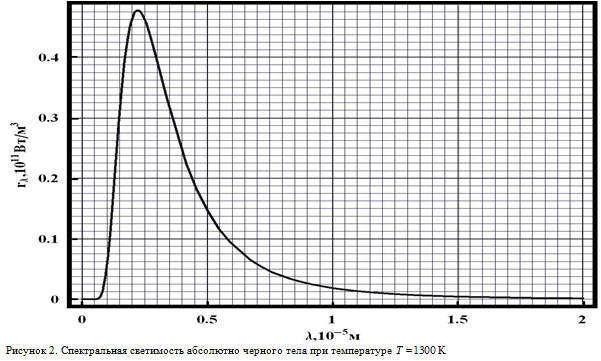
Электромагнитное излучение, испускаемое нагретыми телами, называется тепловым. Тепловое излучение характеризуется интегральной и спектральной светимостью. Интегральной светимостью тела $R$ называется суммарная энергия излучения, ис-пускаемого с единицы площади поверхности тела в единицу времени. Спектральной светимостью тела $r_{\lambda}$ в узком интервале длин волн от $\lambda$ до $\lambda+\Delta \lambda$ называется отношение светимости $\Delta R$ в данном спектральном диапазоне к спектральной ширине этого диапазона $r_{\lambda}=\frac{\Delta R}{\Delta \lambda}$. Интегральная и спектральная светимости тела зависят как от свойств самого тела, так и от его температуры. Светимость тела связана с его способностью поглощать падающее электромагнитное излучение. Чем лучше тело поглощает падающее на него излучение, тем сильнее оно будет излучать при нагревании. Если тело полностью поглощает все падающее на него излучение, то такое тело называется абсолютно черным. Распределение энергии излучения черного тела по спектру (то есть его спектральная светимость) хорошо изучено экспериментально и описано теоретически. На рисунках $1$ и $2$ построены кривые спектральной светимости абсолютно черного тела при двух различных температурах:$T_1=2000$ К (рис. 1) и $T_2=1300$ К (рис. 2).
1. Используя приведенный график зависимости спектральной светимости для температуры $T_1=2000$ К, найдите отношение энергий испускаемых черным телом в спектральных интервалах $(\lambda_1,\lambda_1+\Delta\lambda)$ и $(\lambda_2,\lambda_2+\Delta\lambda)$ для $\lambda_1=2,0\cdot 10^{-6}$ м, $\lambda_2=4,0\cdot 10^{-6}$ м, $\Delta \lambda=0,5 \cdot 10^{-6}$ м. (1 балл)
2. Вин установил, что длина волны $\lambda_{n}$, на которую приходится максимум спектральной светимости, связана с температурой соотношением $$\lambda_{m}=bT^{n},\quad (1)$$ где величина $b$ называется постоянной Вина, $n$ — некоторая целочисленная постоянная. Используя приведенные графики, найдите значения постоянных $b$ и $n$. (2 балла)
3. Стефаном и Больцманом установлено, что интегральная светимость черного тела зависит от температуры по закону $$R=\sigma T^{m}, \quad (2)$$ здесь $\sigma$ — постоянная Стефана-Больцмана,$m$ — некоторая целочисленная постоянная. Используя приведенные графики, найдите значения постоянных $\sigma$ и $m$. (3 балла)
4. Спектральный состав излучения Солнца близок к спектральному составу излучения абсолютно черного тела с $\lambda_{m}=0,48\cdot 10^{-6}$ м. Оцените время, за которое благодаря тепловому излучению, масса Солнца уменьшится на $1\%$. Масса Солнца — $2\cdot 10^{30}$ кг, его радиус $7\cdot 10^8$ м. (4 балла)
комментарий/решение
Электромагнитное излучение, испускаемое нагретыми телами, называется тепловым. Тепловое излучение характеризуется интегральной и спектральной светимостью. Интегральной светимостью тела $R$ называется суммарная энергия излучения, ис-пускаемого с единицы площади поверхности тела в единицу времени. Спектральной светимостью тела $r_{\lambda}$ в узком интервале длин волн от $\lambda$ до $\lambda+\Delta \lambda$ называется отношение светимости $\Delta R$ в данном спектральном диапазоне к спектральной ширине этого диапазона $r_{\lambda}=\frac{\Delta R}{\Delta \lambda}$. Интегральная и спектральная светимости тела зависят как от свойств самого тела, так и от его температуры. Светимость тела связана с его способностью поглощать падающее электромагнитное излучение. Чем лучше тело поглощает падающее на него излучение, тем сильнее оно будет излучать при нагревании. Если тело полностью поглощает все падающее на него излучение, то такое тело называется абсолютно черным. Распределение энергии излучения черного тела по спектру (то есть его спектральная светимость) хорошо изучено экспериментально и описано теоретически. На рисунках $1$ и $2$ построены кривые спектральной светимости абсолютно черного тела при двух различных температурах:$T_1=2000$ К (рис. 1) и $T_2=1300$ К (рис. 2).
1. Используя приведенный график зависимости спектральной светимости для температуры $T_1=2000$ К, найдите отношение энергий испускаемых черным телом в спектральных интервалах $(\lambda_1,\lambda_1+\Delta\lambda)$ и $(\lambda_2,\lambda_2+\Delta\lambda)$ для $\lambda_1=2,0\cdot 10^{-6}$ м, $\lambda_2=4,0\cdot 10^{-6}$ м, $\Delta \lambda=0,5 \cdot 10^{-6}$ м. (1 балл)
2. Вин установил, что длина волны $\lambda_{n}$, на которую приходится максимум спектральной светимости, связана с температурой соотношением $$\lambda_{m}=bT^{n},\quad (1)$$ где величина $b$ называется постоянной Вина, $n$ — некоторая целочисленная постоянная. Используя приведенные графики, найдите значения постоянных $b$ и $n$. (2 балла)
3. Стефаном и Больцманом установлено, что интегральная светимость черного тела зависит от температуры по закону $$R=\sigma T^{m}, \quad (2)$$ здесь $\sigma$ — постоянная Стефана-Больцмана,$m$ — некоторая целочисленная постоянная. Используя приведенные графики, найдите значения постоянных $\sigma$ и $m$. (3 балла)
4. Спектральный состав излучения Солнца близок к спектральному составу излучения абсолютно черного тела с $\lambda_{m}=0,48\cdot 10^{-6}$ м. Оцените время, за которое благодаря тепловому излучению, масса Солнца уменьшится на $1\%$. Масса Солнца — $2\cdot 10^{30}$ кг, его радиус $7\cdot 10^8$ м. (4 балла)
комментарий/решение