5-я Жаутыковская олимпиада (2009), теоретический тур
Эта задача состоит из четырех частей, не связанных друг с другом.
1А (2 балла).
1В (3 балла).
1C (2 балла).
1. Выразите неизвестное сопротивление $R_{x}$ через сопротивления $R_1$, $R_2$, $R_0$ при условии сбалансированности моста.
2. В реальных измерениях практически невозможно точно зафиксировать отсутствие тока через миллиамперметр, так как его чувствительность ограничена. Пусть минимальное значение силы тока, которое может зафиксировать миллиамперметр равно $i_0$ (то есть при $i1D (3 балла).
Солнечным утром на освещаемом солнцем сухом асфальте видны блестящие пятна, похожие на лужи воды. Их появление является простейшим миражом — реально в этих «лужах» мы видим отражение неба.
Цель данной задачи дать теоретическое описание этого явления.
Показатель преломления воздуха $n$ зависит от концентрации молекул $\gamma$ в соответствии с формулой $$n=1+\frac{\alpha \gamma}{2},\quad (1)$$
где $\alpha=2,3\cdot 10^{-29}$ м$^3$ — средняя поляризуемость молекул воздуха. Будем считать, что температура воздуха равна $t_0=20^{\circ}$ С, атмосферное давление $P_0=1,0\cdot 10^5$ Па. Благодаря солнечным лучам у поверхности асфальта образуется тонкий слой более нагретого воздуха, температура которого на $\Delta t=2,0^{\circ}$ С выше, чем температура более высоких слоев.
Водитель движется прямолинейно по горизонтальной дороге, причем его глаза находятся на высоте $h=1,2$ м над поверхностью асфальта. Оцените, на каком расстоянии от водителя он может увидеть ближайшую к нему лужу-мираж.
Постоянная Больцмана $k_{B}=1,38\cdot 10^{-23}$ Дж/К.
При решении данных задач вы можете использовать приближенные формулы справедливые при малых значениях $x$:
$$(1+x)^{\gamma} \thickapprox 1+\gamma x$$
$$\sin x\thickapprox x$$
$$\cos x\thickapprox 1-\frac{x^2}{2}$$
посмотреть в олимпиаде
1А (2 балла).
1В (3 балла).
1C (2 балла).
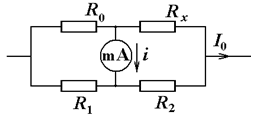
1. Выразите неизвестное сопротивление $R_{x}$ через сопротивления $R_1$, $R_2$, $R_0$ при условии сбалансированности моста.
2. В реальных измерениях практически невозможно точно зафиксировать отсутствие тока через миллиамперметр, так как его чувствительность ограничена. Пусть минимальное значение силы тока, которое может зафиксировать миллиамперметр равно $i_0$ (то есть при $i
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.