Республиканская олимпиада по физике 2015, 10 класс, теоретический тур
Задача №1. (10,0 балла)
Эта задача состоит из трех независимых частей.
Часть 1А
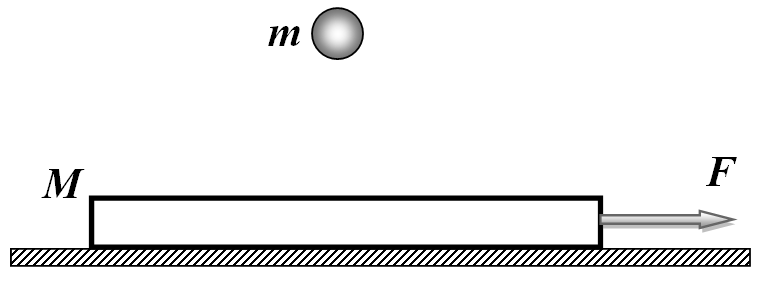
Пластинка массы $M=11,5$ кг движется по шероховатой поверхности (коэффициент трения $k=0,25$) под действием горизонтально направленной силы $F=30$ Н. На пластинке вертикально прыгает шарик массой $m$ так, что средняя скорость пластинки остается постоянной. Считая время удара пренебрежимо малым, найдите $m$. Ускорение свободного падения равно $g=10$ м/с$^2$.
Часть 1B
В электрической схеме, показанной на рисунке в начальный момент времени ключ разомкнут. Найдите какой заряд пройдет через ключ, если его замкнуть. Емкости конденсаторов $C_1$ и $C_2$, сопротивления $R_1$ и $R_2$, а также напряжения источника $U$ считайте известными. Внутреннее сопротивление источника равно нулю.
Часть 1С
Расстояние между прямым изображением, даваемым тонкой линзой, и предметом равно половине фокусного расстояния линзы. Найдите увеличение, с которым изображается предмет.
комментарий/решение
Эта задача состоит из трех независимых частей.
Часть 1А
Пластинка массы $M=11,5$ кг движется по шероховатой поверхности (коэффициент трения $k=0,25$) под действием горизонтально направленной силы $F=30$ Н. На пластинке вертикально прыгает шарик массой $m$ так, что средняя скорость пластинки остается постоянной. Считая время удара пренебрежимо малым, найдите $m$. Ускорение свободного падения равно $g=10$ м/с$^2$.
Часть 1B
В электрической схеме, показанной на рисунке в начальный момент времени ключ разомкнут. Найдите какой заряд пройдет через ключ, если его замкнуть. Емкости конденсаторов $C_1$ и $C_2$, сопротивления $R_1$ и $R_2$, а также напряжения источника $U$ считайте известными. Внутреннее сопротивление источника равно нулю.

Часть 1С
Расстояние между прямым изображением, даваемым тонкой линзой, и предметом равно половине фокусного расстояния линзы. Найдите увеличение, с которым изображается предмет.
комментарий/решение
Задача №2. Газовый цилиндр (10,0 балла)
Газ неон с молярной массой $\mu=20$ г/моль и температурой $T_0=293$ К находится в сосуде под поршнем, который прикреплен к крышке сосуда пружиной жесткости $k=1$ кН/м. Длина пружины в недеформированном состоянии совпадает с высотой сосуда, площадь поперечного сечения которого равна $S=10$ см$^2$. Начальное расстояние от поршня до дна сосуда составляет $x_0=5$ мм, его масса — $m=1$ кг, масса сосуда $M=3$ кг, универсальная газовая постоянная равна $R=8,31$ Дж/(моль$\cdot$К). Сосуд теплоизолирован от окружающей среды, а действием силы тяжести можно пренебречь.
комментарий/решение(1)
Газ неон с молярной массой $\mu=20$ г/моль и температурой $T_0=293$ К находится в сосуде под поршнем, который прикреплен к крышке сосуда пружиной жесткости $k=1$ кН/м. Длина пружины в недеформированном состоянии совпадает с высотой сосуда, площадь поперечного сечения которого равна $S=10$ см$^2$. Начальное расстояние от поршня до дна сосуда составляет $x_0=5$ мм, его масса — $m=1$ кг, масса сосуда $M=3$ кг, универсальная газовая постоянная равна $R=8,31$ Дж/(моль$\cdot$К). Сосуд теплоизолирован от окружающей среды, а действием силы тяжести можно пренебречь.
- Найдите давление газа в сосуде;
- Найдите массу газа, находящегося в сосуде;
- До какой температуры $T$ надо нагреть газ, чтобы расстояние между поршнем и дном сосуда увеличилось вдвое?
- Какое количество теплоты $Q$ надо сообщить газу, чтобы расстояние между поршнем и дном сосуда увеличилось вдвое?
- Рассчитайте теплоемкость газа под поршнем и выразите ее в единицах универсальной газовой постоянной $R$;
- Вычислите частоту $\omega$ малых колебаний поршня возле положения равновесия $x_0$;
- Сосуд повернули набок и положили на гладкую горизонтальную плоскость. Найдите частоту $\omega_0$ малых колебаний поршня в этом случае.

комментарий/решение(1)
Задача №3. Черный ящик (10,0 балла)
комментарий/решение
- В электрической схеме, показанной на рисунке, все вольтметры одинаковые и имеют сопротивление $R=1,00$ кОм. Найдите показания всех вольтметров, если к ним подключен идеальный источник с напряжением $\varepsilon=9,00$ В;
- Какой элемент обязательно находится внутри черного ящика?
- Найдите максимальную мощность, развиваемую черным ящиком;
- Найдите напряжение $\varepsilon$ источника, при котором черный ящик развивает максимальную мощность. Чему равны при этом показания вольтметров?
- Найдите показания вольтметров при напряжении источника равном нулю;
- Найдите показания вольтметров при напряжении источника равном $\varepsilon=3$ В;
- Найдите напряжение источника, при котором сила тока в черном ящике максимальна;
- Найдите показания вольтметров при напряжении источника равном $\varepsilon=2,1$ В;
- Максимальное напряжение источника, при котором сила тока не равна нулю.



комментарий/решение