Математикадан республикалық олимпиада, 2008-2009 оқу жылы, 9 сынып

$ABC$ үшбұрышында іштей сызылған шеңбер $BC$, $CA$ және $AB$ қабырғаларын сәйкесінше $A_1$, $B_1$ және $C_1$ нүктелерінде жанап өтеді. $AC_1B_1$ және $CA_1B_1$ үшбұрыштарының ортоцентрлерін сәйкесінше $H_1$ және $H_2$ арқылы белгілесек, онда $AH_1H_2C$ төртбұрышына сырттай шеңбер сызуға болатынын дәлелдеңіз.

Комментарий/решение

Биссектриса и высота в равнобедренном треугольнике совпадают , то есть $AH_{1};CH_{2}$ есть высоты и биссектрисы , значит они пересекаются в центре вписанной окружности. Положим что высоты равны $C_{1}M;A_{1}N$ .Соединим ортоцентры $H_{2}H_{1}$ , для не обобщения , положим что $C_{1}M>A_{1}N$, опустим перпендикуляр из точки $H_{2}$ на прямую $C_{1}M$ , и равна $L$. $H_{1}M=AB_{1} \cdot cosA \cdot tg(\dfrac{A}{2}),\ \ H_{2}N=CB_{1} \cdot cosC \cdot tg(\dfrac{C}{2})$ так же $AB_{1}(1-cosA)=MB_{1}, \ \ CB_{1}(1-cosC)=NB_{1}$,$H_{2}L=MN$.Учитывая что $r$-радиус , $AB_{1}=r \cdot ctg(\dfrac{A}{2}),\ \ CB_{1}=r \cdot ctg(\dfrac{C}{2})$. Получим соотношение из $\Delta H_{2}H_{1}L$ ,$ctg(H_{2}H_{1}M)=tg(\dfrac{C-A}{2})$ , $H_{2}H_{1}M=90^{o}-\dfrac{C-A}{2}$ , $H_{2}CN=\dfrac{C}{2}$ , $AH_{2}M=\dfrac{A}{2}$.

То есть выполняется соотношения для четырехугольника $AH_{1}H_{2}C=>$ , $ H_{2}H_{1}M+AH_{1}M+H_{2}CN=180^{o}$.

Лемма: симметрии ортоцентра $H$ треугольника $\Delta ABC$ относительно сторон $AB, BC, CA$ будут лежать на описанной окружности этого треугольника.

Пусть $\angle BAC=2\alpha $ и $\angle ACB=2\beta$. Тогда понятно что $AI$ и $CI$ делят эти углы пополам. Также $\Delta AC_{1}B_{1}$ и $\Delta CA_{1}B_{1}$ равнобедренные, из этого $AI$ и $CI$ сер. перпендикуляры для $C_{1}B_{1}$ и $A_{1}B_{1}$ пересекающие их в $M$ и $N$ соответственно. Тогда $A_{1}H_{1}$ и $I$ на одной прямой и $C_{1}H_{2}$, $I$ тоже. Очевидно $AB_{1}IC_{1}$ - вписанный и $CA_{1}IB_{1}$- тоже.

Тогда по нашей лемме симметрии $H_{1}$ и $H_{2}$ относительно $B_{1}C_{1}$ и $A_{1}B_{1} $ переходят в $I$. Отсюда $H_{1}M=MI$ и $H_{2}N=NI$. Тогда если $\angle B_{1}CA_{1}=2\beta $, то $\angle B_{1}C_{1}A_{1}=90-\beta $. $MN$ параллельна $C_{1}A_{1}$ так как она средняя линия $\Delta B_{1}C_{1}A_{1}$.

Тогда $\angle B_{1}MN=90-\beta $. Также $C_{1}B_{1}\perp MI.$ Тогда $\angle IMN=180-\angle NMB_{1}-\angle C_{1}MI=180-90-90+\beta =\beta $.Также $MN$ средняя линия для $\Delta H_{1}H_{2}I$. Значит $MN\parallel H_{1}H_{2}$ и $\angle IH_{1}H_{2}=\beta $.

Значит $\angle AH_{1}H_{2}=180-\beta $. Выходит сумма прот. углов равна 180. $\blacksquare $

легенда написала решение без синусов

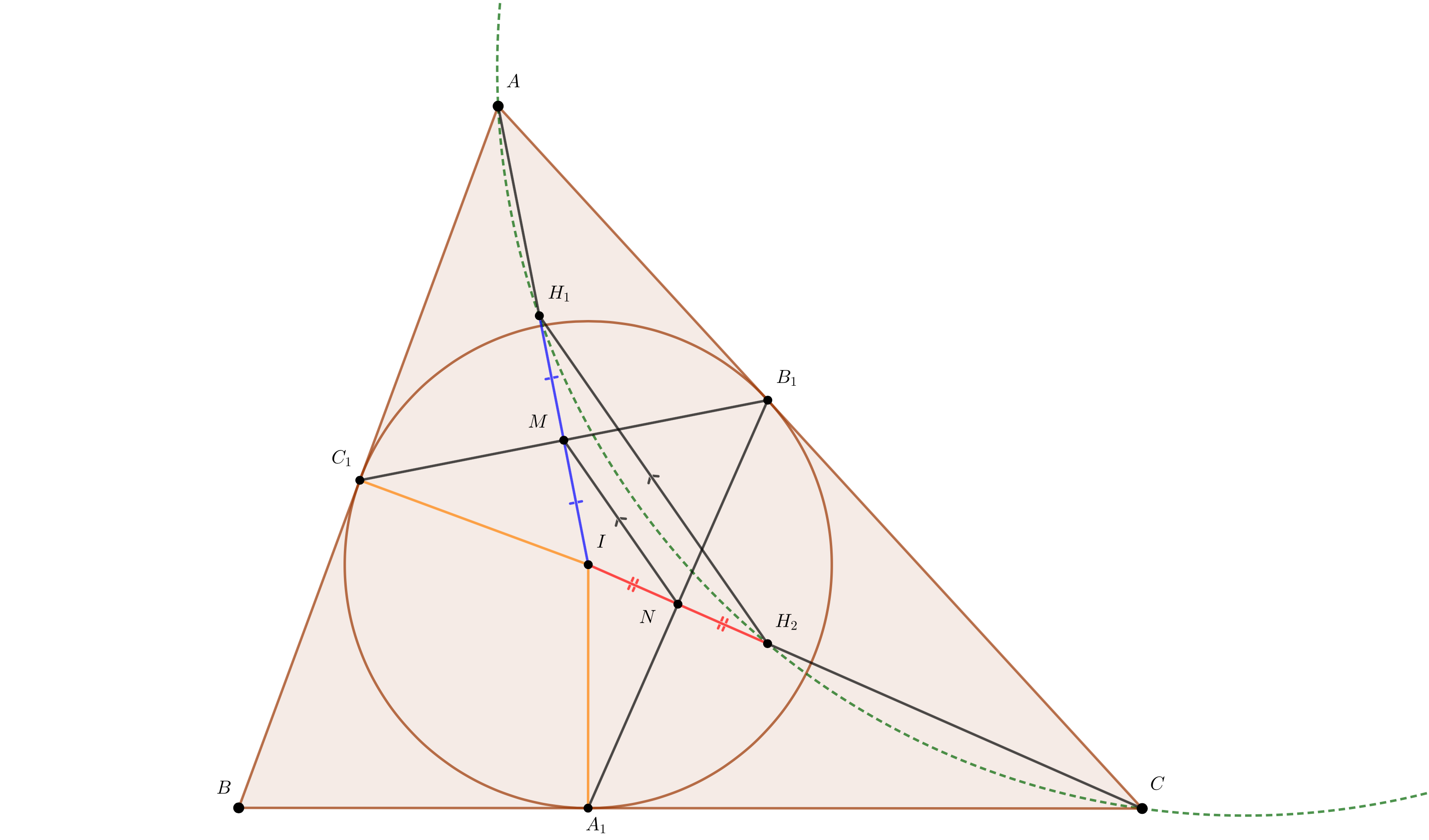
Пусть $M$ и $N$ - середины отрезков $B_1C_1$ и $A_1B_1$. По причинам указанным сверху, $A, H_1, I, M$ лежат на одной прямой. А также $H_1M=IM$ т.к. $H_1$ - ортоцентр и $H_1$ и $I$ симметрично относительно $B_1C_1$. Аналогично $IN=NH_2$. Тогда $MN$ средняя линия треугольника $IH_1H_2$, поэтому $H_1H_2\parallel MN$. Чтобы доказать вписанность $AH_1H_2C$, мы хотим доказать, что $H_1H_2$ и $AC$ антипарралельны относительно угла $\angle AIC$. Поэтому достаточно доказать, что $MN$ и $AC$ антипарралельны или же $MNAC$ вписанный. Из $\triangle AC_1I$ находим, что $IM\times IA=IC_1^2=r^2$. Аналогично $IN\times IC=IC_1^2=r^2$. Поэтому:

$$IM\times IA=r^2=IN\times IC$$

откуда выходит, что $MNAC$ вписанный.$\blacksquare$