10-я международная Иранская олимпиада по геометрии, 2023 год, первая лига, 7-8 классы

Төменгі суреттегі барлық көпбұрыштар — дұрыс көпбұрыштар. $ABCD$ — теңбүйірлі трапеция екенін дәлелдеңіз.

Комментарий/решение

Хорошая задача

Обозначим за $O$ вершину треугольника $AOC$

Заметим, что треугольники $AOD=BOC$ равны.

Следовательно,

$\angle DAO=\angle CBO$

так же заметим что

$\angle OAB=\angle OBA$

таким образом

$AB||CD$

$AD=BC$

значит $ABCD$ - равнобедренная трапеция.

Нужно ещё доказать что это трапеция

Спасибо что подметили

Можете как то по другому назвать точки а то вы использовали одно обозночение на две разные точки.

какие именно?

Чё вы накинулись на него

https://photos.app.goo.gl/f5WtGqHHtaeKUezD8 рисунок геомы

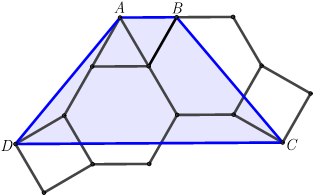
$Возьмём \: \angle BCQ \: как \: \alpha, \: то \: \angle WCN =90- \alpha \: (т.к. \: все \: многоугольники \: правильные). \: \angle FNC=360°- \angle WCN- \angle CWF - \angle WFN= 90+ \alpha \rightarrow \angle EBN = 360 - \angle FNB - \angle NFE - \angle FEB=30+ \alpha \rightarrow \angle CBG= 90- \alpha. \: Соединим \: точки \: G \: и \: C \: и \: выйдет \: то \: что \: \angle BGC=90° \: т.к. \: \angle CBG= 90- \alpha, \angle BCQ= \alpha. \: Далее \: нужно \: заметить \: равенство \: треугольников \: BGC \: и \: AGD, \: они \: равные \: потому \: что \: AG=BG, DM=QC, GM=GQ \: (потому \: что \: \angle GHM = \angle GKQ, GH=HM=GK=KQ), \: и \: \angle AGD = BGC = 90° \: (\angle AGD= \angle AGH + \angle HGM = 60°+(180- \angle GHM):2= 90° \rightarrow \angle ADG = \angle BCG = \alpha, \angle GAD= \angle CBG = 90- \alpha. \: GD=GC, \: \angle CGD = \angle MGK + \angle QGK= 90°+30°=120° \rightarrow \: GDC \: равнобедренный, \: \angle GDC= \angle GCD = 30°. \: И \: на \: последок \: Докажем \: их \: параллельность \: сторон \: AB=CD \rightarrow \angle A + \angle D = 150- \alpha + 30 + \alpha= 180° \: аналогично \: и \: с \: противоположной \: боковой \: стороной. \: Значит \: AB||CD, AD=BC \rightarrow \: ABCD \: равнобедренная \: трапеция.$